Ray Optics and Optical Instruments
Reflection of Light by Spherical Mirrors
- Light is a form of energy which causes sensation of vision.
- Light is an electromagnetic wave
- Light travels with a speed of 3 × 108 m/s in vacuum.
- Light travels with different speeds in different media.
- In reflection, incident ray, reflected Light ray and normal drawn to the surface lie in the same plane.
- Angle of incidence = Angle of reflection
- Angle of deviation = 180 – 2i
- When the rays reflection if actually converge to the image it is called real image
- When the light rays appear to diverge from the image it is called Virtual image.
- Real image can be received on a screen but not the virtual image.
- From principles of sign conversion all distances are measured. From the pole of the mirror.
- The distances measured along the direction of incident light one taken as positive and those measured in the direction opposite to the direction of incident light are taken as negative.
- For spherical mirrors the heights measured upwards and normal to the principal axis are taken as positive & measured downwards are taken as negative.
- Magnification \tt m = \frac{size \ of \ image}{size \ of \ object}
- The image formed by a plane mirror is unmagnified, virtual and erect
- The image is laterally inverted.
- The minimum height of the plane mirror to observe full height of a person is half the height of that person.
- If the object moves with a velocity “V” towards or away from the mirror, then image appears to move with a velocity “2V” toward or away from the mirror.
- When a plane mirror is rotated through an angle “θ” the reflected ray rotates through an angle “2 θ”.
- Two mirrors are placed at an angle of “θ” the angle of deviation produced by a system = 360° − 2 θ.
- If the reflecting surface of the mirror is towards the centre of the spherical surface then it is called concave mirror
- If the reflecting surface of the mirror is away from its centre, then it is called convex mirror.
- Principal axes is the line joining the pole and the centre of curvature
- Focal length (f) is the distance between pole and principal focus.
- Focal length \tt F = \frac{Radius \ of \ curvature}{2}
- Mirror equation \tt \frac{1}{f} = \frac{1}{v} + \frac{1}{u}
- If position of object is at infinity – Nature and position of image is Real, Inverted diminished at focus
- If position of object is beyond centre of curvature Nature and position of image is Real, inverted, diminished between C and F (C = centre of curvature, F = Focus).
- If position of object is at ‘C’ nature and position of image formed is Real, inverted same size as object at C.
- If position of object is between focus and pole nature and position of image formed is virtual, Erect, magnified and behind the mirror between pole and focus.
- If position of object is at focus (F). Nature of Reflected rays are parallel and image formed at infinity.
- \tt \frac{1}{v} and \frac{1}{u} graph is
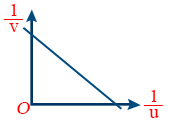
- u-v graph
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Images by two inclined plane mirrors : When two plane mirrors are inclined to each other at an angle θ, then number of images (n) formed of an object which is kept between them.
(i)n = \left[\frac{360^{o}}{\theta} - 1\right]; \ {\tt If} \ \frac{360^{0}}{\theta} = even integer
(ii) If \frac{360^{0}}{\theta} = odd integer then there are two possibilities
2. Mirror formula by Spherical mirror Reflection : \frac{1}{f} = \frac{1}{v} + \frac{1}{u}
3. When object lies along the principal axis then its axial magnification m = \frac{I}{O} = \frac{-(v_{2} - v_{1})}{(u_{2} - u_{1})}
4. If object is small; m = -\frac{dv}{du} = \left[\frac{v}{u}\right]^{2} = \left[\frac{f}{f - u}\right]^{2} = \left[\frac{f - v}{f}\right]^{2}

