Magnetism and matter
The Earth's Magnetism
- When a magnet with magnetic moment M is suspended in a uniform field of induction B at an angle θ with the field direction then the couple (C) acting on the magnet is given by C = MB sin θ
\tt \overrightarrow{C}=\overrightarrow{M}\times\overrightarrow{B} - When θ=90°, C is maximum
\tt\mid \overrightarrow{C}_{max}\mid=MB - When θ=0° (or) 180°\tt\mid \overrightarrow{C}_{min}\mid=\overrightarrow{0}
- Two magnets of magnetic moments M1 and M2 are joined in the form of a cross and this arrangement is pivoted so that it is free to rotate in a horizontal plane under the influence of earth’s magnetic field.
If θ is the angle made by the magnetic meridian with M1 then
\tt \tan\theta = \frac{M_{2}}{M_{1}}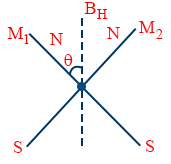
- The Potential Energy of a bar magnet of magnetic \tt \overrightarrow{M} moment placed in a uniform magnetic field \tt \overrightarrow{B} is given by \tt U=-\overrightarrow{M}\cdot\overrightarrow{B}\ U=-MB\cos \theta
- The work done in deflecting a magnet from angular positions θ1 to an angular positions θ2 with the field is given by W = ΔU
W = Δ U (or) W = MB (cos θ1 – cos θ2) - The work done in deflecting a bar magnet through an angle θ from its stable equilibrium position in a uniform magnetic field is given by W= MB (1 – cos θ)
- The magnetic potential at a point due to a bar magnet is, \tt V=\frac{\mu_{0}}{4\pi}\ \frac{M\cos\theta}{r^{2}}
- The time period of vibrating magnet is \tt n =2\pi\sqrt{\frac{I}{MB_{H}}}
- Frequency of vibrating magnet, \tt T=\frac{1}{2\pi}\sqrt{\frac{MB_{H}}{I}}
Where \tt I=m\left(\frac{l^{2}+b^{2}}{12}\right) is moment of inertia of the bar magnet about the axis of oscillation.
M = magnetic moment of the magnet
BH = horizontal component of earths magnetic field - A thin bar magnet is oscillating in a magnetic field, its time period is T
If magnet is cut into ‘n’ equal parts, parallel to length then time period of each part remains same T1 = T - If magnet is cut into ‘n’ equal parts perpendicular to length then time period of each part is \tt T\ '=\frac{T}{n}
- Two magnets of magnetic moments M1 and M2 (M1 > M2) are placed one over the other. If T1 is time period when like poles touch each other and T2 is the time period when unlike poles touch each other, then \tt \frac{M_{1}}{M_{2}}=\frac{T_2^2+T_1^2}{T_2^2-T_1^2}
- In terms of frequencies, \tt \frac{M_{1}}{M_{2}}=\frac{n_1^2+n_2^2}{n_1^2-n_2^2}
- At a given place, the angle between geographical meridian and magnetic meridian is called as MAGNETIC DECLINATION (θ).
- The angle of dip (δ) at a place is defined as the angle made by the direction of earths magnetic field with the horizontal direction in magnetic meridian
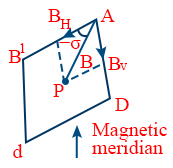
- At a place on poles, earth’s magnetic field is perpendicular to the surface of earth, i.e δ = 90°
Therefore, BV=B sin 90° = B and BH = B cos 90° = 0 - At a place on equator, earth’s magnetic field is parallel to the surface of earth. i.e., δ = 0°
Therefore, BH = B cos 0° = B and BV = BH sin 0° = 0 - \tt \tan\delta=\frac{B_V}{B_H}
- \tt \tan\delta=\frac{B_V}{B'_H}=\frac{B_{V}}{B_{H}\cos \theta}
- \tt \tan\delta_{1}=\frac{\tan\delta}{\cos\theta}\ \left(\because \tan\delta=\frac{B_{V}}{B_{H}}\right)
- If two poles of pole strengths m1 and m2 (m1 < m2) are separated by distance d, then the distance of neutral point from the first pole m1 is
\tt X=\frac{d}{\sqrt{\frac{m_{2}}{m_{1}}\pm1}}
+ for linke poles, − for unlike poles. - If two short bar magnets of magnetic moments M1 and M2 (M1 < M2) are placed along the same line with like poles facing each other and ‘d’ is the distance between their centers, the distance of null point from M1 is
\tt X=\frac{d}{\left(\frac{M_{2}}{M_{1}}\right)^{1/3}\pm1}
+ null point formed between the magnets, − for null point formed outside the magnets. - When a short bar magnet is placed in the earth’s magnetic field with its north pole towards geographic north, then two null points are formed on the equatorial line, one on either side at equal distances from mid point of the magnet. At null point \tt \overrightarrow{B}=\overrightarrow{-B}_{H},\ \ B_{H}=\frac{\mu_{0}}{4\pi}\ \frac{\mu}{d^{3}}
- If ‘m’ is the pole strengths and ‘d’ is the distance from the pole of the magnet where the neutral point is formed then \tt B_{H}=\frac{\mu_{0}}{4\pi}\ \frac{m}{d^{2}}
- \tt B=\mu_{0}H in vacuum
B = μH = μ0 μr H in any medium. - The magnetic moment per unit volume or pole strength per unit area
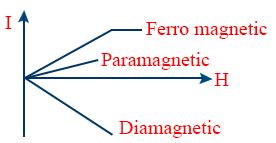
\tt I=\frac{M}{V}=\frac{2l}{2l}\cdot\frac{m}{a}=\frac{m}{a} - The ratio of magnitude of intensity of magnetisation (I) in a material to that of magnetising field (H) is called MAGNETIC SUSCEPTIBILITY of that material (x) x = I/H
- When a magnetic material is placed in a magnetising field for its magnetisation the field inside the magnetic material is the resultant of the magnetising field \tt \overrightarrow{B}_{0} and the induced field \tt \overrightarrow{B}_{i}\ i.e, \overrightarrow{B}=\overrightarrow{B}_{0}+\overrightarrow{B}_{i}\Rightarrow\mu_{r}=1+x
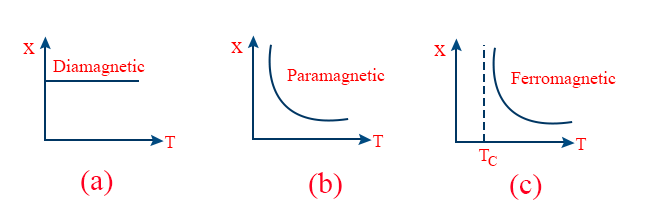
- CURIE’S LAW : The magnetic susceptibility of paramagnetic substances is inversely proportional to absolute temperature. i.e, \tt \chi\propto\frac{1}{T}\Rightarrow\chi=\frac{c}{T}
- CURIE – WEISS LAW : At temperatures above Curie temperature the magnetic susceptibility of ferromagnetic materials is inversely proportional to (T − Tc)
\tt \chi\propto\frac{1}{T-T_{c}}\Rightarrow\chi=\frac{c}{T-T_{c}} - Susceptibility – absolute temperature graph (curve)
- The variation of magnetisation intensity with magnetising force for a ferro magnetic material is shown in hysteresis graph
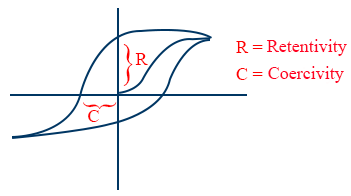
- Intensity of magnetisation I = magnetising, field-H curve
- The retentivity or remanence is defined as the intensity of magnetisation remaining in the substance when the magnetising field has been reduced to zero.
- The COERCIVITY is a measure of the magnetising field intensity required to destroy the residual magnetism in the specimen.
- When a ferro-magnetic substance is taken through a cycle of magnetisation and demagnetisation some energy is lost, which is called HYSTERESIS LOSS.
- The loss of energy per unit volume of specimen per cycle of magnetisation in C.G.S system, is equal to area of I-H loop of specimen. In SI system it is equal to B-H loop.
- The shape and size of I-H or B-H loops depends on the nature of material of specimen.
- The Hysteresis loop help to study the properties like retentivity, coercivity, permeability, susceptibility and energy loss etc.
- The Hysteresis loop help us to select an apt material for different purposes i.e for electromagnets transformer cores, permanent magnets etc.
- The substances which retain their ferromagnetic property for a long period of time are called PERMANENT MAGNETS.
- A permanent magnet should have both large retentivity and coercivity along with high permeability.
- Cobalt, alnico, ticonal, steel etc are the best suited material, steel is mostly preferred for making permanent magnets because its coercivity is large.
- The substances that have low retentivity, low coercivity and small hysteresis loss are called TEMPORARY MAGNETS
- The soft magnets are used for making electromagnets, cores of transformers, motors and generators.
- Stalloy, mu-metal, soft iron are examples of ferromagnetic materials.
- Giant electromagnets are used in cranes to life machinery and bulk quantities of steel and iron.
- Permanent magnets are used in galvanometres voltmeters ammeters, microphones, loud speakers telephones etc
View the Topic in this video From 00:18 To 07:23
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
The equatorial magnetic field of short dipole
B_{E} = \frac{\mu_{0}m}{4 \pi r^{3}}

