Magnetism and matter
The Bar Magnet, Magnetism and Gauss's Law
- A piece of matter, which when suspended freely rests itself in a particular direction (north-south) and which possesses a net magnetic moment and which attracts pieces of ferromagnetic materials like iron, cobalt, Nickel etc towards it, is called a MAGNET.
- A piece of magnet is dipped in iron fillings, they cling to it, especially at certain points. These points are called the poles of the magnet.
- The straight line joining the two poles of a bar magnet is called axial line.
- The line passing through the midpoint normal to the axial line is called equatorial line.
- The force between two isolated magnetic poles is expressed by \tt F=\frac{\mu_{0}}{4\pi}\ \frac{m_{1}m_{2}}{d^{2}}
- \tt F_{Medium}=\frac{\mu}{4\pi}\ \frac{m_{1}m_{2}}{d^{2}}. When the poles are in air or vacuum.
μ0 = permeability of free space
m1, m2 = pole strengths of the pole
SI unit of pole strength = A-m - Relative permeability of the medium
\tt \mu_{r}=\frac{Permeability\ of\ the\ medium}{Permeability\ of\ air\ or\ vacuum}\ \frac{\mu}{\mu_{0}}
μr has no units and no dimensions - Two magnetic poles of same strength (m) are placed at two vertices of an equilateral triangle of side ‘d’ the force on a similar magnetic pole on third corner is given by \tt F^{1}=\sqrt{3}\ \frac{\mu_{0}}{4\pi}\ \frac{m^{2}}{a^{2}}
- Two unlike magnetic poles of same strength (m) are placed at two vertical of an equilateral triangle of side ‘d’. If a north pole of same strength is placed at the third vertex, it experiences a force of magnitude which is given by \tt F^{1}= \frac{\mu_{0}}{4\pi}\ \frac{m^{2}}{a^{2}}
- Four like poles each of pole strength ‘m’ are kept at the four corners of a square of side ‘d’ The net magnetic force on the pole at any one corner is given by \tt F^{1}= \frac{\mu_{0}}{4\pi}\ \frac{m^{2}}{a^{2}}\left[\sqrt{2}+\frac{1}{2}\right]
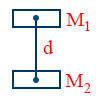
- Force between two co-axial magnetic dipoles \tt F= \frac{\mu_{0}}{4\pi}\ \frac{6\ M_{1}M_{2}}{d^{4}}
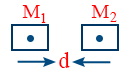
- The force between two parallel magnets \tt F= \frac{\mu_{0}}{4\pi}\ \frac{3\ M_{1}M_{2}}{d^{4}}
- The distance between the two poles of a magnet is called magnetic length of a magnet. It is generally represented as ‘2l’.
- It is directed along the south pole to north pole and it is a vector.
- Magnetic length = \tt \frac{5}{6} × geometric length
- Magnetic Moment (M) is measured as the product of magnetic length and pole strength. M = 2l × m.
- When a bar magnet is cut into ‘n’ equal parts parallel to its axis
Pole strength of each part = M1 = M/n
Length of each part = (2l)1 = 2l
Magnetic moment of each part M1 = M/n - When a bar magnet is cut into ‘n’ equal parts normal to its axis
Pole strength of each part = M1 = M
Length of each part = 2 l/n
Magnetic moment of each part M1 = M/n - When a bar magnet is cut into ‘xy’ equal parts ‘x’ parts parallel to its axis and ‘y’ parts normal to the axis.
- Pole strength of each part M1 = m/x
- Length of each part (2l)1 = 2l/y
- Magnetic moment of each part M2=M/xy
- When two magnets of magnetic moments M1 and M2 are kept at an angle ‘θ’ with like poles touching each other, then the resultant magnetic moment
\tt M^{1}=\sqrt{M_{1}^{2}+M_{2}^{2}+2M_{1}M_{2}\cos \theta} - When two magnets of magnetic moments M1 and M2 are kept at an angle ‘θ’ with unlike poles touching each other, then the resultant magnetic moment.
\tt M^{1}=\sqrt{M_{1}^{2}+M_{2}^{2}-2M_{1}M_{2}\cos \theta} - On bending a magnet its pole strength remains unchanged where as its magnetic moment changes.
- When a thin bar magnet of magnetic moment ‘M’ and length ‘2l’ is bent oil its midpoint with and angle ‘θ’ between the two parts its effective length becomes 2l Sin θ/2
- Its new magnetic moment \tt M^{1}=M\ \sin\frac{\theta}{2}
- When a magnetised wire of length ‘2l’ and magnetic moment ‘M’ is bent in to an arc of a circle, that makes an angle ‘θ’ at the centre of the circle. Its magnetic moment decreases and becomes
\tt M^{1}=\left[\frac{2\ M\ \sin\left(\theta/2\right)}{\theta}\right] where θ is in radian - Like in electric field, the intensity of magnetic induction at a point in a magnetic field is defined as force experienced by a unit north pole placed at that point in magnitude as well as direction.
\tt \overrightarrow{B}=\frac{\overrightarrow{F}}{m},B=\frac{\mu_{0}}{4\pi}\cdot\frac{m}{d^{2}} - S.I unit \tt \overrightarrow{B} is Tesla or weber /m2
- Dimensional Formula of B is [MT−2I−2]
- The magnetic induction at the centre of the line joining the two poles of a horse shoe magnet of pole strength ‘m’ and separated by a distance ‘d’ is
\tt B=8\ \frac{\mu_{0}}{4\pi}\ \frac{m}{d^{2}} directed from N to S pole - A magnetic line of force is the path followed by a free unit north pole in a magnetic field. Magnetic field can be represented by magnetic lines of force. They are imaginary.
- Two magnetic lines of force never intersect; if they intersect it means that field has two directions at the point of intersection which is impossible.
- The magnetic field, in which the magnetic induction field strength is same both in magnitude and direction at all points, is known as UNIFORM MAGNETIC FIELD.
- The magnetic field, in which the magnetic induction or field strength differs either in magnitude or in direction or both is known as NON UNIFORM MAGNETIC FIELD.
- Magnetic flux (Φ) linked through a cross section is defined as dot product of \tt \overrightarrow{B}\ and\ \overrightarrow{A}\ \ \phi=\overrightarrow{B}\cdot\overrightarrow{A}\ =BA\ \cos \theta
Where θ = angle made by magnetic field \tt \overrightarrow{B} with the normal to the area \tt \left(\hat{n}\right)\ \overrightarrow{A}=A\hat{n} A = area of the coil - B at a point ‘P’ on the axial line of a bar magnet at a distance ‘d’ from the centre of the magnet is \tt B_{a}=\frac{\mu_{0}}{4\pi}\ \frac{2Md}{\left(d^{2}-l^{2}\right)^2}
- B at a point ‘P’ on the equatorial line of a bar magnet at a distance ‘d’ from the centre of the magnet is \tt B_{e}=\frac{\mu_{0}}{4\pi}\ \frac{M}{\left(d^{2}+l^{2}\right)^3/2}
- In cast of short magnet \tt B_{e}=\frac{\mu_{0}}{4\pi}\frac{M}{d^3}\ \left(\therefore l<<d\right)
- Magnetic Induction at a points ‘P’ and whose position vector from the mid point of the magnet makes an angle θ with magnetic axis is given by \tt B_{e}=\frac{\mu_{0}}{4\pi}\frac{M}{d^3}\sqrt{1+3\cos^{2}\theta}
- If θ=0° \tt B=\frac{\mu_{0}}{4\pi}\ \frac{2M}{d^3}(Axial line)
- If If θ=90° \tt B=\frac{\mu_{0}}{4\pi}\ \frac{M}{d^3}(equatorial line)
View the Topic in this video From 01:06 To 56:05
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. The far axial magnetic field of a bar magnet which one may obtain experimentally. Thus, a bar magnet and a solenoid produce similar magnetic fields.
B = \frac{\mu_{0}}{4\pi} \frac{2m}{r^{3}}
2. The torque of the dipole in a magnetic field τ = m × B
3. In a simple hormonic motion, the square of angular frequency is and time period is
T = 2p \sqrt{\frac{I}{mB}} \ {\tt or} \ B = \frac{4 p^{2}I}{mT^{2}}
4. The Gauss's law of electrostatics, the flux through a closed surface in that case is given by
\sum E \cdot \Delta S = \frac{q}{\varepsilon_{0}}
5. Gauss's law of magnetism states that the flux of B through any closed surface is always zero \int_{s} B·ds = 0
6. Gauss's law of electrostatics, \int_{s} B·ds = μ0 qm where qm is the magnetic charge

