Electromagnetic Induction
Motional Electromotive Force and Eddy Current
If a rod of length l moves perpendicular to a magnetic field B, with a velocity v ,then induced emf produced in it given by
E = B . v × l = B v l
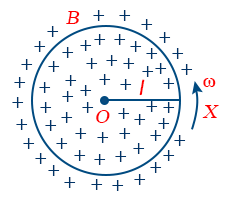
If a metallic rod of length l rotates about one of its ends in a plane perpendicular to the magnetic field, then the induced emf produced across its ends is given by
E = 1/2 Bωl2
If a metallic disc of radius r rotates about its own centre in a plane perpendicular to the magnetic field B, then the induced emf produced between the centre and the edge is given by
E = 1/2 Bωr2
Eddy Currents:
If a piece of metal is placed in a varying magnetic field or rotated with high speed in a uniform magnetic field , then induced current set up in the piece are like whirlpool of air called eddy currents. These are also known as Facault’s current.
i = - e/R
View the Topic in this video From 01:11 To 25;06
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. If rod is moving by making an angle θ with the direction of magnetic field or length, induced emf e = Bvl sin θ
2. If conducting rod moves on two parallel conducting rails as in time t distance travelled by conductor = vt
Area generated A = lvt. Flux linked with this area Φ = BA = Blvt. Hence induced emf |e| = \frac{d\phi}{dt} = Bvl
3. Induced current : i = \frac{e}{R} = \frac{Bvl}{R}
4. Magnetic force : Conductor PQ experiences a magnetic force in opposite direction of it's motion and F_{m} = Bil = B\left[\frac{Bvl}{R}\right]l = \frac{B^{2}vl^{2}}{R}
5. Power dissipated in moving the conductor : For uniform motion of rod PQ, the rate of doing mechanical work by external agent or mech. power delivered by external source is given as P_{mech} = P_{ext} = \frac{dW}{dt} = F_{ext}.v = \frac{B^{2}vl^{2}}{R} \times v = \frac{B^{2}v^{2}l^{2}}{R}
6. Cycle wheel : In a conducting wheel each spoke of length l is rotating with angular velocity ω in a given magnetic field as
e_{net} = \frac{1}{2} B\omega l^{2}; \omega = 2\pi v
7. Induced emf in coil : Induced emf also changes in periodic manner that's why phenomenon called periodic EMI.
e = -\frac{d\phi}{dt} = NBA \ \omega \sin \omega t

