Communication Systems
Amplitude Modulation, Production and Detection of Amplitude Modulated Wave
- During PHASE MODULATION, the phase of the CW (carrier wave) is changed in accordance with the amplitude variations of the signal.
- The extent to which the modulation is to be taken up is called the modulation factor (ma)
- \tt m_{a} = \frac{Amplitude \ change \ in \ carrier \ wave}{Amplitude \ of \ unmodulated \ CW}
- If a carrier wave is modulated by different audio waves to different strengths then the effective modulation factor is given by \tt \sqrt{m_{1}^{2} + m_{2}^{2} + ....}
- Carrier Wave power \tt P_{c} = \frac{V_{c}^{2}}{2R}
- Power of each side band \tt P_{1} = \frac{m_{a}^{2} V_{c}^{2}}{8R}
- Total power of side bands \tt P_{s} = \frac{m_{a}^{2} V_{c}^{2}}{4R}
- Total power carried by modulated wave \tt P_{T} = \frac{V_{c}^{2}}{2R} + \frac{m_{a}^{2} V_{c}^{2}}{4R} = \frac{V_{c}^{2}}{2R} \left[\frac{2+m_{a}^{2}}{2}\right]
- Fractional power carried by the side bands \tt \frac{P_{S}}{P_{T}} = \frac{m_{a}^{2}}{2 + m_{a}^{2}}
- \tt \frac{P_{C}}{P_{T}} = \left(\frac{I_{c}}{I_{t}}\right)^{2}
- \tt \frac{P_{S}}{P_{T}} = \frac{m_{a}^{2}}{2 + m_{a}^{2}} = \frac{1}{3}
- \tt \frac{P_{C}}{P_{T}} = \frac{2}{2 + m_{a}^{2}} = \frac{2}{3}
- y(t) = BVm sin ωmt + BVc sin ωct + \tt \frac{CV_{m}^{2}}{2} + \frac{V_{c}^{2}}{2} - \frac{CV_{m}^{2}}{2} \cos 2 \omega_mt - \frac{CV_{c}^{2}}{2} \cos 2 \omega_{c}t + CVm Vc cos (ωc − ωm)t − CVm Vc cos (ωc + ωm)t
-
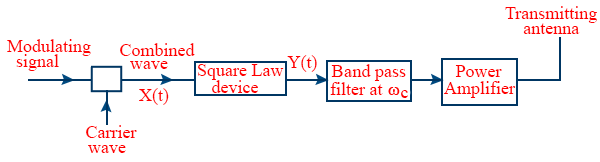
- Detection:

View the Topic in this video From 00:24 To 23:24
View the Topic in this video From 00:11 To 2:19
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Power in Amplitude Modulation waves Power dissipated in any circuit, P = V^{2}_{rms}/R. Hence,
Carrier power, P_{c} = \frac{(E_{c}/\sqrt{2})^{2}}{R} = \frac{E_{c}^{2}}{2R}
2. Total power of Amplitude modulation wave,
P_{t} = P_{c} + P_{sb} = \frac{E_{c}^{2}}{2R}\left[1 + \frac{m_{a}^{2}}{2}\right]
3. A sinusoidal carrier wave can be represented as
c(t) = Ac sin (ωct + Φ)

