Solid State
Calculations involving unit cell parameters and Imperfection in solids
- Cell parameters: A unit cell can be characterised by two types of parameters
(i) It's dimension along three edges a, b and c
(ii) angles between the edges α (between b & c)
β (between a & c)
γ (between a & b) - It can be represented as follows.
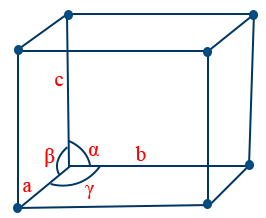
- Calculations involving unit cell parameters:
Let a = length of edge of a unit cell
r = radius of atom (point)
rank of unit cell ← z = Number of atoms in unit cell
d = density of unit cell
NA = Avogadro's number
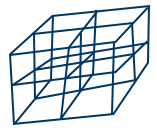
M = Molecular mass of unit cell - Contribution of an atom to unit cell from corner of a cubic crystal lattice is "\frac{1}{8}" since atom at corner of cubic unit cell shared by 8 neighboring unit cells.
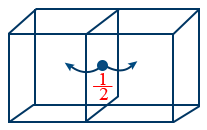
- Contribution of an atom to unit cell from face centre is \frac{1}{2} since atom at face centre is shared by two neighboring unit cells.
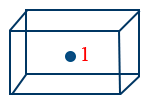
- Contribution of an atom to unit cell from body centre is 1 since one full atom at centre of unit cell.
- Contribution of an atom to unit cell from edge centre is \frac{1}{4} since atom at edge centre is shared by four neighboring unit cells.
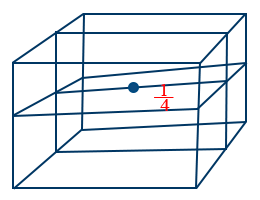
- Number of atoms in primitive cubic unit cell is 1
Number of atoms = 8 \times\frac{1}{8}=1 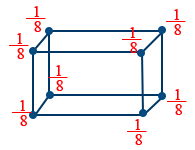
- Number of atoms in one F.C.C unit cell is Z = 4

Z(effective) = From all the corners = 8 \times\frac{1}{8}=1
From all the face centres = 6 \times\frac{1}{2}=\frac{3}{4}
Rank (or) Zeffective (or) Z = 4- Number of atoms in one B.C.C unit cell Zeff = 2
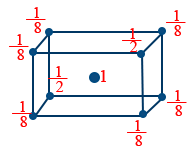
Z(effective) = From all the corners = 8 \times\frac{1}{8}=1
From body centres = 1 \times 1=\frac{1}{2}- Trick to calculate Zeffective for cubic unit cell.
Z_{eff}=\frac{C}{8}+\frac{B}{1}+\frac{F}{2}+\frac{E}{4}
C = Number of atoms from all corner
B = Number of atoms from body centre
F = Number of atoms from all available faces
E = Number of atoms from all available edges - Density of a unit cell can be calculated by using following formula d=\frac{ZM}{N_{A}a^{3}}
- Relations between "a" and "r" of unit cells
(1) For F.C.C atoms touch along face diagonal 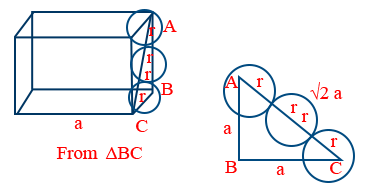
- \therefore 4r = \sqrt{2}a
a = 2\sqrt{2}r - For B.C.C atoms touch along body diagonal
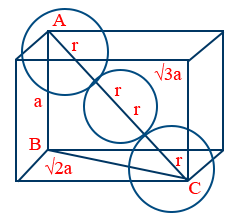
- \therefore 4r = \sqrt{3}a
a = \frac{4}{\sqrt{3}}r - For simple cubic atoms touch along edge length

- ∴ a = 2r
Part1: View the Topic in this Video from 0:07 to 12:08
Part2: View the Topic in this Video from 0:08 to 10:57
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
Bragg's equation, nλ = 2d sinθ
where, n = 1, 2, 3......(diffraction order)
λ = wavelength of X - rays incident on crystal and
d = distance between atomic planes
θ = angle at which interference occurs.

