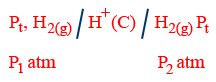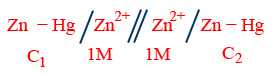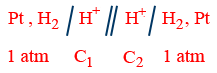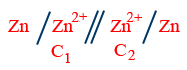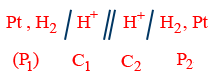Electrochemical, Electrolytic and Galvanic cells and Electrolysis, Electrodes and Electrode Potential

Electrochemical cells:
(a) It is a physical set-up (a device) which is used to convert the chemical energy of an indirect spontaneous redox reaction into electric energy i.e. electricity.
(b) The de-electronation (oxidation) takes place at anode which gives electrons in the external circuit and electronation (reduction) takes place at cathode. Internal circuit is completed by a porous material (or) a salt bridge.
Note: If porous material is used that electrochemical cell is called Daniel cell.
If salt bridge is used that electrochemical cell is called Galvanic cell.
(c) Salt bridge: It is U-shaped tube contains saturated solution of inert electrolyte like KCl, KNO₃, NH₄Cl and NH₄NO₃ etc in agar-agar gel
(i) cation and anion of inert electrolyte have same mobility
(ii) Ions of inert electrolyte do not mix with electrolytic solution present in the half cell.
(iii) Ions of inert electrolyte do not participate in electrochemical change.
(d) Functions of salt bridge:
(i) It complete the electrical circuit.
(ii) It maintained the two half cell electrically neutral by the flow of ions.

Electrode: An object (may be metal (or) gas with metal) which acts as sink or source of electrical energy is called electrode.
These are of various types (i) Inert electrode (Au, Pt), (ii) Reactive electrode (iii) Gas electrodes

Electrode potential: When a metal rod ((or) non metal also) is dipped in a solution of its own ions electronation (or) de-electronation takes place as a result potential develops electrode and electrolyte.
∴ The potential difference between electrode and the electrolyte is called electrode potential. Standard electrode potential: Electrode potential measured at 25°C and 1M concentration of electrolytic solution is called standard electrode potential.
(a) In case of gaseous electrode 1 atm pressure is taken as standard.
(b) Standard oxidation potential is represented as SOP/E_{ox}^o/E_M^\infty/M^{n+}
     Standard reduction potential is represented as SRP/E_{red}^o/E_{M^{n+}}^\infty/M
(c) In general standard electrode potential means S.R.P Factors influencing electrode potential:
(1) Nature of the electrode
(2) Temperature
(3) Activity (Concentration (or) Pressure)

For a particular electrode at a particular temperature and activity oxidation and reduction potentials are having equal magnitude and opposite in sign.
OP = −RP
E_Oxi = −E_Red
E_{M/M^{+n}}=E_{M^{+n}/M}

EMF of a cell (E_cell) :
E_cell = E_Oxi(Anode) + E_Red(Cathode)
E_cell = −E_Red (Anode) + E_Red(Cathode)
       = E_{Right cell} − E_{Left cell} Concentration cell: Anode and cathode both are formed by same substance so E_{cell}^o=0, such type of cell is known as concentration cell. Concentration gradient may arise either in electrode material (or) in electrolyte. Thus there are two types of concentration cell. (I) Electrode concentration cell:
(i) Electrode gas concentration cell:

E_{cell}=\frac{0.0591}{2}\log \frac{P_{1}}{P_{2}}
(ii) Electrode (metal) concentration cell:

E_{cell}=\frac{0.0591}{2}\log \frac{C_{1}}{C_{2}}

(II) Electrolyte concentration cell: The cell activities of electrodes are same and activities of electrolytes are different.

\therefore E_{cell}=\frac{0.0591}{2}\log \frac{C_{2}}{C_{1}}

\therefore E_{cell}=\frac{0.0591}{2}\log \frac{C_{2}}{C_{1}}

(III) Mixed concentration cell: In these concentration cells activities of both electrodes and electrolytes are different.

\therefore E_{cell}=\frac{0.0591}{2}\log \frac{P_{1}C_2^2}{P_{2}C_1^2}

Applications of concentration cell:
(i) Determination of solubility and solubility product of a sparingly soluble sale:
(Q) Find the solubility and K_SP of saturated solution of Ag₂CrO₄ at 298 K given Ag / Ag₂CrO₄ // AgNO₃(0.1 M) /Ag    E_cell = 0.164 V
                   Ag / Ag⁺(C₁) // Ag⁺(C₂) / Ag
E_{cell}=\frac{0.0591}{1}\log \frac{C_{2}}{C_{1}}
0.164=0.0591 \log \frac{0.1}{C_{1}}
\log \frac{0.1}{C_{1}}=\frac{0.164}{0.0591}=2.7749
\frac{0.1}{C_{1}}=10^{2.775} (or) Anti log (2.7749) = 595.6
C_{1}=\frac{0.1}{10^{2.775}}=1.68\times 10^{-4} (or) C_{1}=\frac{0.1}{59.56}=1.68\times 10^{-4}
Ag_{2}CrO_{4}\rightleftharpoons 2Ag^{+}+CrO_4^{2-}
∴ K_SP = 4S²
But 2S = 1.68 × 10⁻⁴
S = 8.4 × 10⁻⁵ M
∴ K_SP  = 4 × (8.4 × 10⁻⁵)²
= 2.3708 × 10⁻¹²M²
(iii) We can determine P^H of solution Ecell = −0.0591 × P^H Relation between metal-metal ion half cell and metal in soluble salt anion half cell and metal insoluble salt anion half cell

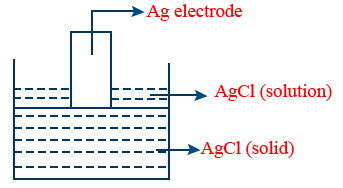
E_{Cl^{-}}^{o}/AgCl/Ag=E_{Ag^{+}/Ag}^o + 0.0591 \log(K_{SP})
K_SP = Solubility Product Electrolysis: Chemical changes in electrolyte solution by passage of electric current, resulting into deposition of metal (or) liberation of gases at electrodes is known as electrolysis. Electrolytic cell: This cell converts electrical energy into chemical energy. The entire assembly except that of the external battery is known as the electrolytic cell. Quantitative aspect of electrolysis:
(i) Faraday's first law of electrolysis: In an electrolytic cell mass of substance deposited (or) liberated at an electrode (cathode)
m=\frac{A \times C\times t}{v\times 96500}
A = Atomic mass of element
C = Current in amperes
t = time in seconds
v = valency of element
Trick: If current efficiency x% is given
          \therefore m=x \% \times\frac{A \times C\times t}{v\times 96500}
(ii) Faraday's second law: When different electrolytic cells are connected in series mass of substances liberated at respective electrodes when same strength of current passes through them is directly proportional to their equivalent masses
\therefore \frac{W_{1}}{W_{2}}=\frac{E_{1}}{E_{2}}

Trick to find product at respective electrodes during electrolysis:
Case (i): In between inert electrodes (Pt) for molten electrolyte cation deposit at cathode, anion liberates at anode.
Case (ii): In between inert electrodes (Pt)
(a) In case of aqueous alkali (or) alkaline earth metal salt solution
      Instead of these metal cation water undergoes reduction at cathode 2H₂O + 2e⁻ → H₂ + 2OH⁻
(b) If anion is oxo anion in aqueous salt solution
      Oxo anion \tt \rightarrow NO_3^{^-},SO_4^{2-},PO_4^{3-}
      OH⁻ Undergoes oxidation at anode
      4OH⁻ → O₂ + 2H₂O + 4e⁻
Case (iii): In case of active electrodes (reactive electrodes) anode will dissolve and that same metal deposits at cathode.