Oscillations and Waves
Some system Executing Simple Harmonic Motion
A point mass suspended from a massless spring or placed on a frictionless horizontal plane attached with spring(fig) constitutes a linear harmonic spring pendulum.
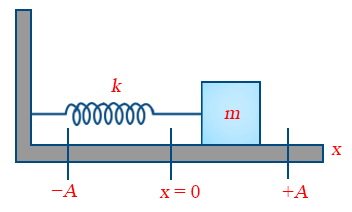
If the point mass is pulled on one side and is released,it then executes a to and fro motion about the mean position.let x=0, indicate the position of the centre of the point mass when the spring is in equilibrium.the positions marked as –A and +A indicate the maximum displacements to the left and the right of the mean position.
At any time t,if the displacement of the point mass from its mean position is x,the restoring force F acting on the block is,
F(x) = - kx
Where k=spring constant
Time period T = 2 \pi \sqrt{\frac{m}{k}}
frequency f = \frac{1}{2 \pi} \sqrt{\frac{k}{m}}
Oscillations due to a spring View the Topic in this video From 0:23 To 5:23
Simple Pendulum View the Topic in this video From 0:39 To 12:40
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. F(t) = ma = − mω2 x(t)
Where, k = mω2 is force constant.
2. At any displacement x,
Potential energy, U = \frac{1}{2}m\omega^{2}x^{2} = \frac{1}{2}kx^{2}
\tt =\frac{1}{2}kA^{2} \cos^{2}(\omega t + \phi)
3. Kinetic energy,
\tt K =\frac{1}{2}mv^{2} =\frac{1}{2} m\omega^{2} A^{2} \sin^{2}(\omega t + \phi)
\tt =\frac{1}{2}kA^{2} \sin^{2}(\omega t + \phi)
4. Total energy, E = K + U = \frac{1}{2}kA^{2}, It always remains constant even though K and U change with time
5. A block of mass m oscillating under the influence of restoring force F = −kx exhibits simple hormonic motion with angular frequency \omega = \sqrt{k/m} and time period T = 2 \pi \sqrt{\frac{m}{k}}
6. The motion of a simple pendulum is simple harmonic whose time period and frequency are given by
T = 2 \pi \sqrt{\frac{L}{g}} \ {\tt and} \ \nu = \frac{1}{2 \pi}\sqrt{\frac{g}{L}}

