Motion in a Plane
Projectile Motion
When any object is thrown from horizontal at an angle θ except 900 , then the path followed by it is called trajectory, the object is called projectile and its motion is called projectile motion.
If any object is thrown with velocity u, making an angle θ from horizontal, then
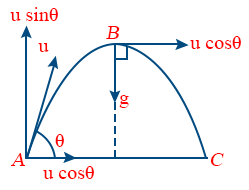
Horizontal component of initial velocity= u cos θ.
Vertical component of initial velocity=u sin θ.
Horizontal component of velocity (u cos θ) remains same during the whole journey as no acceleration is acting horizontally.
Vertical component of velocity (u sin θ) decreases gradually and becomes zero at highest point of the path.
At highest point, the velocity of the body is u cosθ in horizontal direction and the angle between the velocity and acceleration is 900 .
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. At highest point, the linear momentum is mu cos θ and the kinetic energy is \frac{1}{2}m (u \cos \theta)^{2}.
2. The horizontal displacement of the projectile after t seconds x = (u cos θ)t
3. The vertical displacement of the projectile after t seconds y = (u \sin \theta)t - \frac{1}{2}gt^{2}
4. Equation of the path of projectile y = x \tan \theta - \frac{g}{2u^{2} \cos^{2}\theta}x^{2}
5. Kinetic energy at lowest point = \frac{1}{2}mu^{2}
6. Linear momentum at lowest point = mu
7. Angular momentum of projectile = mu cos θ × h, where h denotes the height.
8. Time of flight is the total time for which the projectile remains in air. T = \frac{2u \sin \theta}{g}
9. Maximum height is the maximum vertical distance covered by projectile. H = \frac{u^{2} \sin^{2} \theta}{2g}
10. Horizontal range is the maximum distance covered in horizontal distance. R = \frac{u^{2} \sin 2\theta}{g}
11. Horizontal range is maximum when it is thrown at an angle of 45° from the horizontal R_{max} = \frac{u^{2}}{g}
12. Projectile Projected from Some Heights:
When Projectile is Projected Horizontally
Initial velocity in vertical direction = 0
Time of flight T = \sqrt{\frac{2H}{g}}
Horizontal range x = uT = u\sqrt{\frac{2H}{g}}
Vertical velocity after t seconds vy = gt
Velocity of projectile after t seconds v = \sqrt{v_{x}^{2} + v_{y}^{2}} = \sqrt{u^{2} + (gt)^{2}}
If velocity makes an angle Φ from horizontal, then \tan \phi = \frac{v_{y}}{v_{x}} = \frac{gt}{u}
Equation of the path of the projectile y = -\frac{g}{2u^{2}}x^{2}
13. When Projectile Projected Downward at an Angle with Horizontal
Initial velocity in horizontal direction = u cos θ
Initial velocity in vertical direction = u sin θ
Time of flight can be obtained form the equation, H = u \sin \theta t + \frac{1}{2} gt^{2}
Horizontal range x = (u cos θ)t
Vertical velocity after t seconds vy = u sin θ + gt
Velocity of projectile after t seconds v = \sqrt{v_{x}^{2} + v_{y}^{2}} = \sqrt{(u \cos \theta)^{2} + (u \sin \theta + gt)^{2}}
= \sqrt{u^{2} + (gt)^{2} + 2ugt \sin \theta}
14. When Projectile Projected Upward at an Angle with Horizontal
Initial velocity in horizontal direction = u cos θ
Initial velocity in vertical direction = u sin θ
Time of flight can be obtained from the equation H = (-u \sin \theta)t + \frac{1}{2}gt^{2}
Horizontal range x = (u cos θ)t
Vertical velocity after t seconds, vy = (− u sin θ) + gt
Velocity of projectile after t seconds
v = \sqrt{v_{x}^{2} + v_{y}^{2}} = \sqrt{u^{2} + (gt - u \sin \theta)^{2}}
= \sqrt{u^{2} + (gt)^{2} - 2ugt \sin \theta}
15. Projectile Motion on an Inclined Plane
Initial velocity along the inclined plane = u cos (α − β)
Initial velocity perpendicular to the inclined plane = u sin (α − β)
Acceleration along the inclined plane = g sin β
Acceleration perpendicular to the inclined plane = g cos β
Time of flight T = \frac{2u \sin (\alpha - \beta)}{g \cos \beta}
Horizontal range x = \frac{2u^{2} \sin (\alpha - \beta) \cos \alpha}{g \cos \beta}
Range on inclined plane R = \frac{x}{\cos \beta} = \frac{2u^{2} \sin (\alpha - \beta) \cos \alpha}{g \cos^{2}\beta}
Range on inclined plane will be maximum, when \alpha = 45^{0} + \frac{\beta}{2}
R_{max} = \frac{u^{2}}{g(1 + \sin \beta)}

