Ray Optics and Optical Instruments
Refraction through a Prism, Dispersion by a Prism
- Prism is a transparent piece having two refracting surfaces with non zero angle between them.
- In prism Angle of prism A = r1 + r2
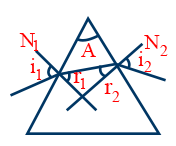
- In prism Angle of Deviation d = i1 + i2 – A.
- Condition for minimum deviation in prism i1 = i2 = i3, r1 = r2 = r.
- Refractive index of prism with respect to surroundings \tt \mu = \frac{\sin \frac{A + D_{m}}{2}}{\sin \frac{A}{2}}
- Condition for normal incidence and grazing emergence i1 = r1 = 0 i2 = 90° & r2 = c = A.
- For grazing emergence \tt A = C = \sin^{-1} \left(\frac{1}{\mu}\right)
- Condition for grazing incident and grazing Emergence i1 = i2 = 90° r1 = r2 = C A = 2C d = 180° − 2C
- In order to have an Emergent ray the maximum angle of prism is “2 c” which is called Limiting angle of prism.
- Condition for total internal reflection at second face of prism sin (i) = \tt \sqrt{\mu^{2} - 1} (sin A – cos A)
- Deviation angle for small angled prisms d = (μ t)A
- Deviation angle for small angled prisms in medium \tt d = \left(\frac{\mu g}{\mu m}t\right) A
- The separation of composite beam of light into constituent colours is called Dispersion.
- In Dispersion the angle of refraction is most for red and least for violet (r v < r R)
- In Dispersion Angle of deviation is most for Violet and least for red (dv > dR)
- In Dispersion the refractive index is most for violet and least for red (μv > μR)
- The difference between angles of deviation for any pair of colours is called angular dispersion. θ = δV – δR.
- Dispersive power of medium (ω) is the ratio between angular dispersion and mean angle of deviation. \tt \omega = \frac{\theta}{\delta y} = \frac{\delta v - \delta R}{\left(\frac{\delta v + \delta R}{2}\right)}
- The deviation of yellow is taken as Mean deviation of violet and red \tt \omega = \frac{\delta v - \delta R}{\delta y}
- Angular dispersion o for small angles prisms θ = δv – δR = (μv – μR) A.
- Dispersive power for small angles prisms \tt \omega = \frac{\theta}{\delta y} = \frac{\delta v - \delta R}{\delta y} = \frac{\mu v - \mu R}{\mu y - 1}
- Condition for deviation without dispersion. θ + θ1 = 0 (or) ωδ + ω1δ1 = 0.
- Net deviation = δ + δ1 = (μ − 1)A + (μ1 − 1) A1
- Condition for Dispersion without deviation is δ + δ1 = 0 (or) (μ − 1) A + (μ1 − 1) A1 = 0
- Net dispersion = θ + θ1 = ωδ + ω1δ1
- Law of refraction at spherical surface \tt \frac{\mu_{2}}{v} - \frac{\mu_{1}}{u} = \frac{\mu_{2} - \mu_{1}}{R}
- Lens makers formula \tt \frac{1}{f} = \left(\frac{\mu_{2}}{\mu_{1}} - 1\right) \left(\frac{1}{R_{1}} - \frac{1}{R_{2}}\right)
- For diverging miniseus \tt \frac{1}{f} = \left(\frac{\mu_{2}}{\mu_{1}} - 1\right) \left(\frac{1}{R_{1}} - \frac{1}{R_{2}}\right)
- For converging minisens \tt \frac{1}{f} = \left(\frac{\mu_{2}}{\mu_{1}} - 1\right) \left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)
- For convex lens \tt \frac{1}{f} = \left(\frac{\mu_{2}}{\mu_{1}} - 1\right) \left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)
- For concave lens \tt \frac{1}{f} = \left(\frac{\mu_{2}}{\mu_{1}} - 1\right) \left(\frac{1}{R_{1}} +\frac{1}{R_{2}}\right)
- The focal power (P) of a lens is numerically equal to the reciprocal of its focal length \tt P = \frac{1}{f} (diopters)
- If two lenses are separated by a distance “d” \tt \frac{1}{f} = \frac{1}{f_{1}} + \frac{1}{f_{2}} - \frac{d}{f_{1} f_{2}}
- P = P1 + P2 - dP1 P2
- When an Equiconvex lens (f) is cut into two plano convex lenses focal length of each becomes “2f”.
- One of the surface of Convex lens is silvered. \tt \frac{1}{F} = \frac{1}{fl} + \frac{1}{fm} + \frac{1}{fl} = \frac{2}{fl} + \frac{1}{fm}
- If plane surface of a Planoconvex lens is silvered \tt \frac{1}{F} = \frac{2}{fl} + \frac{1}{fm}
\tt \frac{1}{F} = \frac{2}{fl} + \frac{1}{\infty}
\tt F = \frac{R}{2 (\mu + 1)}

- If the spherical surface of a planoconvex lens is silvered
\tt \frac{1}{F} = \frac{2}{fl} + \frac{1}{fm}
\tt F = \frac{R}{2 \mu }
- Rainbows are formed by dispersion of sunlight falling on raindrops.
- If the molecules of a medium after absorbing in coming radiations emits in all possible directions this process is called scattering.
View this topic in this Video from 1:08
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
For surface AC \mu = \frac{\sin i}{\sin r_{1}}; For surface AB \ = \frac{1}{\mu} = \frac{\sin r_{2}}{\sin e}

