Moving charges and magnetism
The Solenoid and the Toroid, Force between Two Parallel Currents, the Ampere
- Magnetic induction at a point on the axis of solenoid \tt B = \frac{\mu_{0} n i}{2} (\sin \alpha + \sin \beta)
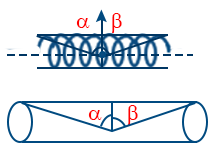
- "B" near one end \tt B = \frac{\mu_{0} ni}{2}
- Magnetic induction at the centre of finite solenoid \tt B = \frac{\mu_{0}}{4 \pi} (4 \pi n i) \sin \alpha\tt and \sin \alpha = \frac{L}{\sqrt{L^{2} + 4 R^{2}}}
- Magnetic induction in toroid \tt B = \frac{\mu_{0}}{2 \pi} . \frac{Ni}{r} (L = 2 \pi r)
- B = \frac{\mu_{0} Ni_{0}}{L}
- Magnetic field inside the core and the field outside the toroid is zero i.e. BQ = 0 and BR = 0.
- Force between two current carrying parallel wires is \tt \frac{F}{l} = \frac{\mu_{0}}{2 \pi} \frac{i_{1} i_{2}}{r}
- If currents in the two wires are in same direction then the force of attraction taken place between them.
- If currents in the two wires are in opposite direction then the force of repulsion taken place between them.
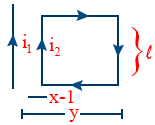
- Force on the loop is \tt F = \frac{\mu_{0} i_{1} i_{2} l}{2 \pi} \left[\frac{1}{x} - \frac{1}{y}\right]
- Force on the hanging wire to remain stationary \tt F = mg = \frac{\mu_{0} i_{1} i_{2} l}{2 \pi r}
\frac{m}{l} = \frac{\mu_{0}i_{1}i_{2}}{2\pi r g}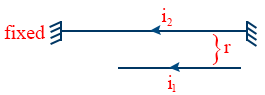
View the Topic in this video From 01;02 To 38;29
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
Force Between Two Parallel Current Carrying Conductors
f = \frac{\mu_{0}}{4 \pi} \frac{2I_{1}I_{2}}{r}

