Electrostatic Potential and Capacitance
Potential due to a Point Charge, Electric Dipole and system of charges
- The potential at a point due to an Electric dipole is \tt V=\frac{P\cos\theta}{4\pi \varepsilon_{0}r^{2}}
- For a point on the axial line is \tt V=\frac{P}{4\pi \varepsilon_{0}r^{2}}
- For a point on the equatorial line is V = O
- The surface over which the potential is same as called equipotential surface
- Electrostatic potential due to infinite long changed wire at “r” \tt V=\frac{\lambda}{2\pi e_{0}}\log_{e}^{r}+\ k {k = constant}
- The Electrostatic Potential due to a thin infinite non conducting plane sheet \tt V=-\frac{\sigma}{2\varepsilon_{0}}r
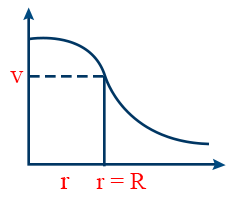
- The Potential at a point outside the sphere is \tt V=\frac{1}{4\pi \varepsilon_{0}}.\frac{Q}{r}=\frac{\sigma\ R^{2}}{\varepsilon_{0}r} (R = Radians)
- The Potential at a point on the surface of sphere \tt V=\frac{1}{4\pi e_{0}}.\frac{Q}{R}=\frac{\sigma\ R}{\varepsilon_{0}}
- The Potential inside the sphere \tt V=\frac{1}{4\pi \varepsilon_{0}}.\frac{Q\left(3R^{2}-r^{2}\right)}{2R^{3}}
- V centre > V surface > V out (sphere)
-
 (Sphere)
(Sphere) - Electric Potential’s unit is volt.
- When 1 Joule of work is done in bringing 1 unit coulomb of charge then the potential is said to be 1 volt.
View the Topic in this video From 01:39 To 36:51
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Potential due to System of charges
Let there be a number of point charges q1, q2, q3, ........ qn at distances r1, r2, r3 ......, rn respectively from the point P, where electric potential is given by
V = \frac{1}{4\pi \varepsilon_{0}}\sum_{i = 1}^{n} \frac{q_{i}}{r_{i}}
2. Potential Gradient
The rate of change of potential with distance in electric field is called potential gradient.
Potential gradient = \frac{dV}{dr}
3. Relation between potential gradient and electric field intensity is given by
E = -\left[\frac{dV}{dr}\right]
4. The net torque experienced by the dipole is
τ = pE sin θ
\overrightarrow{\tau} = \overrightarrow{p} \times \overrightarrow{E}
5. Potential Difference:
V_{ab} = -\int_{a}^{b} \overrightarrow{E}.d \ \overrightarrow{r}
6. Work done in Rotationg an Electric Dipole in a unifrom electric field
⇒ Wexternal = PE(1 − cos θ)

