Alternating Current
LC Oscillations
When a charged capacitor C having an initial charge q0 is discharged through an inductor L, the charge and current in the circuit starts oscillating simple harmonically. If the resistance of the circuit is zero, no energy is dissipated as heat. The total energy associated with the circuit is constant.
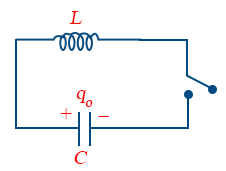
Frequency of oscillation is given by
\omega = \frac{1}{\sqrt{LC}}
View the Topic in this video From 24:43 To 57:40
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Oscillates with a natural frequency \omega_{0} = \frac{1}{\sqrt{LC}}
2. A mass m oscillating with frequency ω0, the equation is \frac{d^{2}x}{dt^{2}} + \omega_{0}^{2}x = 0

