Determinants
Applications of Determinants and Matrices
- The system of equations are said to be homogeneous system of equations if it is in the form
a1x + b1y + c1z = 0
a2x + b2y + c2z = 0
a3x + b3y + c3z = 0
(or)
a1x + b1y = 0
a2x + b2y = 0 - The system of equations are said to be non homogeneous equations, if it is in the form
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
(or)
a1x + b1y = d1
a2x + b2y = d2 - Solution of Homogeneous equations (Ax = 0)

- The system of equations are said to be consistent if it has unique solution (or) infinitely many solutions.
- The system of equations are said to be Inconsistent if it has no solution
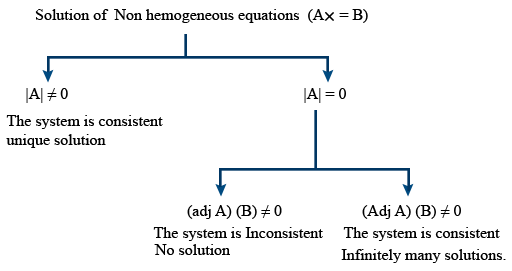
- Solution of Non homogeneous equations (Ax = B)
View the Topic in this video From 00:40 To 56:01
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
- Homogeneous equations
a1x + b1y + c1z = 0
a2x + b2y + c2z = 0
a3x + b3y + c3z = 0 in matrix form is
\begin{bmatrix}a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{bmatrix}\begin{bmatrix}x \\ y \\ z \end{bmatrix} = \begin{bmatrix}0 \\ 0 \\ 0 \end{bmatrix}
Ax = 0 - Non Homogeneous equations
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3 in matrix form is
\begin{bmatrix}a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{bmatrix}\begin{bmatrix}x \\ y \\ z \end{bmatrix} = \begin{bmatrix}d_{1} \\ d_{2} \\ d_{3} \end{bmatrix}
A x = B
A = Coefficient matrix
x = solution matrix - CRAMER'S RULE for solving of system of Non-homogeneous equations:
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
\Delta = \begin{vmatrix}a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{vmatrix}
\Delta_{1} = \begin{vmatrix}d_{1} & b_{1} & c_{1} \\ d_{2} & b_{2} & c_{2} \\ d_{3} & b_{3} & c_{3} \end{vmatrix}
\Delta_{2} = \begin{vmatrix}a_{1} & d_{1} & c_{1} \\ a_{2} & d_{2} & c_{2} \\ a_{3} & d_{3} & c_{3} \end{vmatrix}
\Delta_{3} = \begin{vmatrix}a_{1} & b_{1} & d_{1} \\ a_{2} & b_{2} & d_{2} \\ a_{3} & b_{3} & d_{3} \end{vmatrix}
x=\frac{\Delta_1}{\Delta},y=\frac{\Delta_2}{\Delta},z=\frac{\Delta_3}{\Delta} - MATRIX INVERSION METHOD for solving of Non-homogeneous equations
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
The System of equation in matrix form is
\begin{bmatrix}a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{bmatrix}\begin{bmatrix}x \\ y \\ z \end{bmatrix} = \begin{bmatrix}d_{1} \\ d_{2} \\ d_{3} \end{bmatrix}
A x = B
⇒ x = A−1 B
\tt \Rightarrow x = \frac{1}{|A|}(adj A)(B) - Echelon form of a matrix
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
Argument matrix → \begin{bmatrix}a_{1} & b_{1} & c_{1} & d_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} \\ a_{3} & b_{3} & c_{3} & d_{3} \end{bmatrix}
↓ using Elementary Row operations
Echelon form of matrix → \begin{bmatrix}a_{1} & b_{1} & c_{1} & d_{1} \\ 0 & b_{2} & c_{2} & d_{2} \\ 0 & 0 & c_{3} & d_{3} \end{bmatrix}
Argument matrix → \begin{bmatrix}a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \\ a_{4} & b_{4} & c_{4} \end{bmatrix}
↓ using Elementary column operations
Echelon form of matrix → \begin{bmatrix}a_{1} & 0 & 0 \\ a_{2} & b_{2} & 0 \\ a_{3} & b_{3} & c_{3} \\ a_{4} & b_{4} & c_{4} \end{bmatrix} - Characteristic equation:
If A = \begin{bmatrix}1 & 1 & 0 \\ 1 & 2 & 1 \\ 2 & 1 & 0 \end{bmatrix}, then the characteristic equation is |A − xI| = 0
\Rightarrow \begin{bmatrix}1-x & 1 & 0 \\ 1 & 2-x & 1 \\ 2 & 1 & -x \end{bmatrix} = 0
⇒ x3 − 3x2 − 1 = 0
The characteristic equation is
A3 − 3A2 − I = 0

