Solutions
Solubility and Henry's Law, Ideal and Non-Ideal Solutions, Vapour Pressure and Raoult's Law
Solubility & Henry's law:
Solution of gas in liquid:-
(1) In these solutions gas is solute and liquid is solvent
(2) The solubility of a gas in a liquid is influenced by the following factors.
(a) Nature of the gas:
Easily liquifiable gases (Ex; CO2, SO2, HCl, NH3 etc.,) are more soluble in a solvent when compared with permanent gases, (He, N2, H2, O2)
(b) Nature of liquid :
A gas more soluble in a liquid in which it undergoes either dissociation (or) association.
Ex:- HCl is more soluble in H2O than in C6H6
(C)Temperature:-

Here forward reaction is (dissolution of a gas in liquid) exothermic, According to Le Chatelier principle low 'T' are favourable
(d)Pressure:-

In Forward reaction number of moles of gas decreases
(2) According to Le chatelier principle higher "P" are favourable
(3) Effect of pressure on solubility of a gas in a liquid can be explained by Henry's law
(4) Henry's law:
(a)Definition 1:- At a particular "T" for a given volume of a liquid weight of gas dissolved is directly proportional to it's pressure
w ∝ P ⇒ w = kHP
KH = Henry's constant
w = wt of gas dissolved
P = pressure of the gas
(b)Definition (2):- At a particular "T" for a given volume of a liquid the partial pressure of a gas over a liquid is directly proportional to it's mole fraction in the liquid
P ∝ X(gas)
Pi = KH Xgas
Pi = Partial pressure of the gas over the liquid
KH = Henry's constant
Xgas mole fraction of the gas in liquid
Trick:- (a) According to above Definition "2" higher the KH for a particular gas lesser it's solubility
(b) 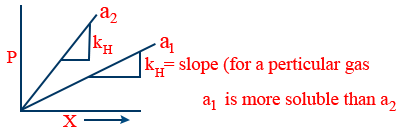
(C) Definition (3):- At a particular T for a given volume of liquid solubility (S) of a gas is directly proportional to partial pressure of gas over the liquid
S ∝ P
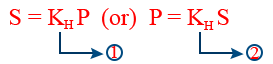
Solubility can be considered as any concentration term like molarity, molality, mole fraction.
Trick:- Selection of formula (1) or (2) depends up on units of "P"
(i) If units of KH = units of "P" we need to consider formula (2)
(ii) if units of KH = (units of P)−1
we need to consider formula (1)
(5) Limitations of Henry's Law:-
(1) Temperature should not be too low
(2) Pressure should not be too high
(3) Gas should not undergo either dissociation (or) association in the liquid.
(4) Gas should not react with liquid.
Vapour pressure and Raoult's law:-
(1) Vapour pressure:- The pressure exerted by a vapour of a liquid over a liquid when it is in equilibrium with the liquid at a particular "T" is called vapour pressure.
(2) Vaporization depends up on
(a) Nature of liquid
(b) Surface area of liquid (It is directly proportional)
(c) Air current over the liquid
(d) Temperature.
(3) But vapour pressure depends upon only temperature
\tt P = K e^{\frac{-\Delta H_{vap}}{RJ}}
(4) 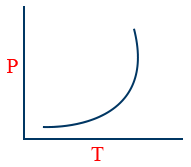
(5) \log \frac{P_{2}}{P_{1}} = \frac{\Delta H_{vap}}{2.303 R}\left[\frac{1}{T_{1}} - \frac{1}{T_{2}}\right]
ΔHvap = Enthalpy of vapourisation
R = Universal gas constant.
(6) Raoult's law for liquid- liquid Binary solution:-
(1) Definition:- For a solution of two/more volatile liquids partial vapour pressure of any liquid in the solution is equal to product of mole fraction of the liquid in the solution and vapour pressure of that pure liquid.
(2) Let us assume a solution is formed by the combination of two volatile liquids A & B
\tt P_{A} = X_{A}P^{o}_{A} ; P_{B} = X_{B}P^{o}_{B}
∴PS = PA + PB
\tt \Rightarrow P_{S} = X_{A}P^{o}_{A} + X_{B}P^{o}_{B}
Where PA & PB are partial vapour pressures of liquids A & B
XA & XB are mole fractions of liquids A & B
\tt P^{o}_{A} \ \& \ P^{o}_{B} are vapour pressure of pure liquids A & B
PS is total vapour pressure of solution.
\tt \therefore P_{S} = (P^{o}_{A} - P^{o}_{B}) X_{A} + P^{o}_{B}
(or)
\tt P_{S} = (P^{o}_{B} - P^{o}_{A}) X_{B} + P^{o}_{A}
(3) Mole fraction of A & B in liquid & vapour state:-
According to Dalton's law of partial pressure
\tt P^{o}_{i} = X_{i}P
PA = YA PS
YA = Mole fraction of A in vapour phase
\tt \Rightarrow Y_{A} = \frac{P_{A}}{P_{S}}
\tt \Rightarrow Y_{A} = \frac{X_{A}P^{o}_{A}}{X_{A}P^{o}_{A} + X_{B}P^{o}_{B}}
similarly \tt Y_{B} = \frac{X_{B}P^{o}_{B}}{X_{A}P^{o}_{A} + X_{B}P^{o}_{B}}
Ideal and non ideal solutions:-
(1) Based on Raoult's law solutions are classified into 2 types
(a) Ideal solution :-
The solution which obeys Raoult's law at all temperature and concentration is called an ideal solution
(b) Non-ideal solution :-
The solution which does not obey Raoult's law at all temperatures and concentrations is called a non-ideal solution.
(2) Non Ideal solutions are again classified into 2 types.
(a) Non-Ideal solution which shows positive deviation from Raoult's law (Type - I)
(b) Non-Ideal solution which shows negative deviation from Raoult's law (Type-II)
(3) Comparison between ideal & non ideal solution can be shown as follows
| Ideal Solution | Type- I solution | Type-II solution | |
| (1) | \tt P_{A} = X_{A}P^{o}_{A} | \tt P_{A} > X_{A}P^{o}_{A} | \tt P_{A} < X_{A}P^{o}_{A} |
| (2) | \tt P_{B} = X_{B}P^{o}_{B} | \tt P_{B} > X_{B}P^{o}_{B} | \tt P_{B} < X_{B}P^{o}_{B} |
| (3) | \tt P_{S} = X_{A}P^{o}_{A} + X_{B}P^{o}_{B} | \tt P_{S} > X_{A}P^{o}_{A} + X_{B}P^{o}_{B} | \tt P_{S} < X_{A}P^{o}_{A} + X_{B}P^{o}_{B} |
| (4) | \tt \Delta H_{mix} \simeq 0 | Δ Hmix > 0 (positive) Endothermic | ΔHmix < 0 (negative) exothermic |
| (5) | \tt \Delta V_{mix} \simeq 0 | ΔVmix > 0 | ΔVmix < 0 |
| (6) | A-B attractions are average of A-A & B-B attractions | A-B attractions are weaker when compared with A-A & B-B attractions | A-B attractions are stronger when compared with A-A & B-B attractions |
| (7) |
|
|
|
Fractional distillation:-
(1) The process of separating component liquids from a solution by using the concept of distillation is called fractional distillation.
(2) During fractional distillation compositions are changed
(3) Fractional distillation is possible at a temperature at which compositions of liquids & vapour phases are different.
(4) Azeotropic mixture:-
(1) An azeotropic mixture behaves as a pure liquid.
(2) A solution of two or more liquid which boils at a particular temperature and distills over completely at that particular temperature without under going any change in composition is called azeotropic mixture.
(3) Azeotrope with maximum vapour pressure and minimum boiling point is formed by the solution which shows positive deviation from Raoult's law
Ex:- 95.57% by mass of Et-OH
(4) Azeotrope with minimum vapour pressure and maximum boiling point is formed by the solution which shows negative deviation from Raoult's law
Ex:- 6.8% by mass of HNO3.
Trick for completely immiscible liquids:
For completely immiscible liquids
(1) \tt P_{A}^{o} = Y_{A}P_{mix}
\tt P_{B}^{o} = Y_{B}P_{mix}
2) \tt \frac{P_{A}^{o}}{P_{B}^{o}} = \frac{Y_{A}}{Y_{B}}
3) \tt \frac{P_{A}^{o}}{P_{B}^{o}} = \left(\frac{n_{A}}{n_{B}}\right)_{vapour phase}
4) \tt \left(\frac{w_{A}}{w_{B}}\right)_{vapour} = \frac{P_{A}^{0}}{P_{B}^{0}} \times \frac{M_{A}}{M_{B}}
Part1: View the Topic in this Video from 0:27 to 59:58
Part2: View the Topic in this Video from 0:07 to 19:05
Part3: View the Topic in this Video from 0:09 to 11:07
Part4: View the Topic in this Video from 0:09 to 8:17
Part5: View the Topic in this Video from 0:07 to 15:38
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Henry's Law \tt p=\left(\frac{1}{k'}\right)x_{2}=k_{H}x_{2}
where kH is known as Henry's law constant.
2. Raoult's Law
\tt p_{total}=p_{A}+p_{B}=x_{A}\ p_{A}^{\star}+x_{B}\ p_{B}^{\star}