Solid State
Seven crystal systems, Nearest neighbours and Point defects
Several crystal systems:
| Sl.No | Crystal Systems | Bravais lattices | Maximum symmetry elements | Parameters of unit cell |
Examples | |
| Intercepts | Crystal Angle | |||||
| 1. | Cubic (Regular) | Primitive F.C.C; B.C.C - 3 | Nine plane of symmetry thirteen axes of symmetry | a = b = c | α = β = γ = 90° | NaCl, Zinc blende Cu, KCl, CaF2, ZnS, Cu2O, Diamond, Alums, Pb, Ag, Au, Mg |
| 2. | Tetragonal | Primitive body centre - 2 | Five plane of symmetry Five axes of symmetry |
a = b ≠ c | α = β = γ = 90° | White Sn, SnO2, CaSO4, TiO2, ZrSiO4, PbWO4, KH2PO4 |
| 3. | Orthorhombic | Primitive F.C.C, B.C.C, E.C.C - 4 | Three plane of symmetry Three axes of symmetry |
a ≠ b ≠ c | α = β = γ = 90° | KNO3, K2SO4, BaSO4, PbCO3, Mg2SiO4, Rhombic sulphur |
| 4. | Hexagonal | Primitive - 1 | Seven plane of symmetry Seven axes of symmetry |
a = b ≠ c | α = β = 90°, γ = 120° | Graphite, ZnO, CdS, Wurtzite, HgS, Ice, PbI2, Beryl, Mg, Zn, Cd |
| 5. | Trigonal {Rhombohedral} | Primitive - 1 | Seven plane of symmetry Seven axes of symmetry |
a = b = c | α = β = γ ≠ 90° | CaCO3 (calcite) HgS, quartz Mn |
| 6. | Monoclinic | Primitive B.C.C - 2 | One plane of symmetry One axis of symmetry |
a ≠ b ≠ c | α = γ = 90°, β ≠ 90° | Na2SO4.10H2O, CaSO4. 2H2O, Monoclinic sulphur |
| 7. | Triclinic | Primitive - 1, Total = 14 | No plane of symmetry No axis of symmetry |
a ≠ b ≠ c | α ≠ β ≠ γ ≠ 90° | K2Cr2O7, H3BO3, CuSO4.5H2O |
- Tricks for several crystal system:
Remember 1st letters C T O H T M T
Remember number of bravais lattices 3 2 4 1 1 2 1
Observe inequality of intercept upto "O" then for remaining it reverse for H, T, last M & T all are unequal.
First 3 crystal angles are equal to 90°.
H γ = 120°,
Trigonal Rhombohedral means Rhombus so α = β = γ ≠ 90°
M γ ≠ 90°
Triclinic either intercept & crystal angle all are not equal. - Point defect: Missing of a point from lattice site during formation of crystal lattice is known as point defect.
- Classification of point defect:
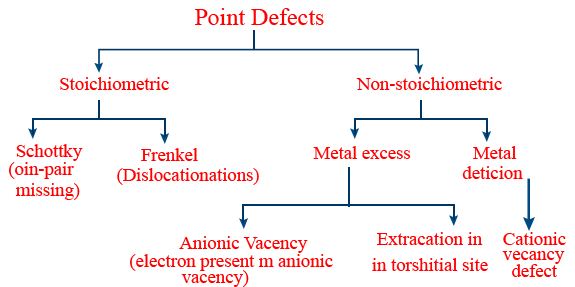
- Stoichiometric defect:
- Vacancy: When constituent particles missing, then vacancy defects occurs.
- Frenkel defect: Ionic compound with low coordination number (4) can show this Eg: AgBr, ZnS
- Schottky: Ionic compound with high coordination number (6 or 8) can show this eg: NaCl.
- Trick: All alkali & alkaline earth metal halides compounds shows schottky defect.
- Due to Frenkel defect density of compound will not change.
- Due to schottky defect density of compound decreases.
- Non-stoichiometric defects:
(1) Metal excess defect: This is due to anion vacancies or due to the presence of extra cations at interstitial site.
Eg: ZnO in hot condition shows this
(2) Metal deficiency defect: This defect is due to absence of positive ion from lattice site or extra interstitial negative ion.
Eg: Ni0.98O1.0; Fe0.93O1.0 - Nearest neighbours:
- The closest distance between centres of two atoms in a crystal lattice is called nearest neighbour.
- Trick to find closest distance
(1) always we need to find 2r value. - Closest distance in simple cubic is a = 2r ⇒ 2r = a
- Closest distance (nearest neighbour) in B.C.C. since atoms touch along body diagonal
\therefore 4r = \sqrt{3} \ a
Nearest neighbour distance is (2r) = \frac{\sqrt{3}}{2} \ a - Nearest neighbour in F.C.C
since atoms touch along face diagonal
4r = \sqrt{2} \ a\Rightarrow 2r = \frac{a}{\sqrt{2}}
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Cationic vacancies produced = [number of cations of higher valence × difference in valence of the host cation and cation of higher valence]

