Electrochemistry
Conductivity and Kohlrausch's Law
- Molar conductance Λmol (or) μc: The conducting power of all the ions of 1 mole of electrolyte present in a solution is called molar conductance.
- Relationship between Λmol & K:
(a) Case (i): Let us assume 1 mole of an electrolyte is present in 1 cm3 of solution
∴ Λmol = K
(b) Case (ii): 1 mole of an electrolyte is present in Vcm3 of solution
∴ Λmol = K × V
(c) Units for Λmol :
ohm−1 cm2 mole−1 (or) S cm2 mole−1 (C.G.S)
ohm−1 m2 mole−1 (or) S m2 mole−1 (M.K.S)
1 S m2 mole−1 = 104 S cm2 mole−1 - Effect of dilution: Upon dilution molar conductance increases
- Relationship between molar conductance & molarity:
(a) Case (i): In C.G.S system \wedge_{mol}=\frac{K\times 1000}{M}
(b) Case (ii): In M.K.S system \wedge_{mol}=\frac{K}{1000\times M} - Relationship between equivalent conductance & molar conductance:
\wedge_{equi}=\frac{K\times 1000}{N}
\wedge_{mol}=\frac{K\times 1000}{M}
\tt \frac{\wedge_{equi}}{\wedge_{mol}}=\frac{GEW}{GMW} - Variation of molar conductance with concentration (or dilution): For both strong and weak electrolytes up on dilution molar conductance increases.
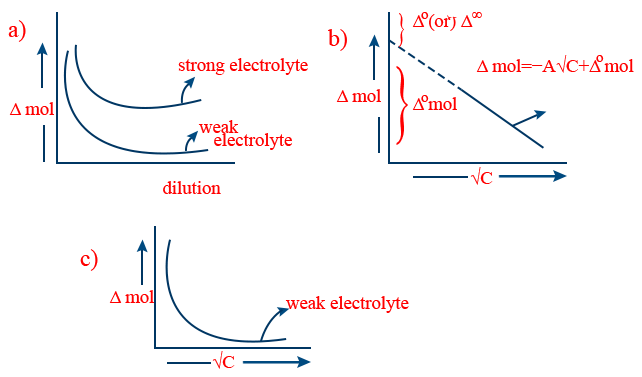
- (i) Λ0 (or) Λ∞ is called limiting molar conductance. This can be determined for a strong electrolyte by extra polation of the curve \tt \wedge \ vs \sqrt{c} towards y-axis
(ii) Λ0 (or) Λ∞ of a weak electrolyte can't be determined by the extra polation of the curve \tt \wedge \ vs \sqrt{c} towards y-axis
(iii) Λ0 of a weak electrolyte can be determined indirectly by using Kohlrausch's law. - Kohlrausch's law of independent migration of ions: At infinite dilution (where 100% dissociation takes place) each ionic species (cation/anion) contributes a fixed value towards molar conductance of an electrolyte irrespective of other ion in combination with it and molar conductance of an electrolyte at infinite dilution is equal to sum of ionic conductance of the contributing ion.
\tt \wedge_{AB}^{^\infty}=\lambda_{A^{+}}^{^\infty}+\lambda_{B^{-}}^{^\infty}
\tt \wedge_{A_{x}B_{y}}^{^\infty}=x\lambda_{A^{y+}}^{^\infty}+y\lambda_{B^{x-}}^{^\infty} - Trick: (i) If equivalent conductance is considered
\tt \wedge_{AB}^{^\infty}=\lambda_{A^{+}}^{^\infty}+\lambda_{B^{-}}^{^\infty}
\tt \wedge_{A_{x}B_{y}}^{^\infty}=\lambda_{A^{y+}}^{^\infty}+\lambda_{B^{x-}}^{^\infty} (No need to multiply with stoichiometric coefficients. According to law of equivalence)
(ii) Molar conductance = (Total charge on cation + anion) × (equivalent conductance) - Applications of Kohlrausch's Law:
(a) Determination of solubility and solubility product of sparingly soluble salt: In case of sparingly soluble salt a very small part of salt is soluble.
∴ Λc = Λ∞
\tt\therefore \wedge_{c}=\wedge_{\infty}=\frac{K\times1000}{M}
\tt\therefore M=\frac{K\times1000}{\wedge_{\infty}}
For sparingly soluble salts (i.e, they always form saturated solutions) molarity is equal to solubility.
∴ S mole L−1 = M
(b) ∴ Ksp = xxyysx + y
(c) Specific conductance are additive in nature.
Ksolution = Ksalt + Kwater
(1) In case of soluble salts
Kwater < < < Ksalt
∴ Kwater is neglected
∴ Ksalt ≈ Ksolution
(ii) In case of sparingly soluble salts Ksalt = Ksolution − Kwater - Ionic mobility (U): The speed of an ion under unit potential gradient is called ionic mobility.
U=\frac{Speed \ of \ an \ ion}{Potential \ gradiant}
U=\frac{Speed \ of \ an \ ion}{\begin{bmatrix}\frac{Potential \ difference\ (PD)}{Distance \ between\ 2\ electrodes\ (DBE)} \end{bmatrix}}
U=\frac{V\times DBE}{PD}
Unit of U: cm2 sec−1 volt−1 - Relationship between ionic mobility and ionic conductance:
\lambda_+^\infty \propto U_+^\infty; \lambda_\ominus^\infty \propto U_\ominus^\infty
\lambda_+^\infty = FU_+^\infty; \lambda_\ominus^\infty = FU_\ominus^\infty F = 9.65 × 104 coulombs
\therefore U^\infty =\frac{\lambda^\infty}{F}
\frac{V^\infty \times DBE}{PD}=\frac{\lambda^\infty}{F}
V^\infty=\frac{\lambda^\infty}{F}\times\frac{PD}{DBE}
↓
Speed of ion at infinite dilution
∴ Distance traveled by an ion at infinite dilution =\frac{\lambda^\infty}{F}\times\frac{PD}{DBE}\times time\ in\ sec
\therefore\wedge_\infty=\lambda_+^\infty+\lambda_-^\infty=F(U_+^\infty+U_-^\infty) - Conductometric titrations:
(a) The titrations in which conductance measurements are made use in the determination of end point of a titration are called conductometric titrations.
(b) Among all the cations, cation with highest ionic conductance is H⊕ i.e, \lambda_{H+}^\infty = 349.8 ohm−1 cm2 mole−1
Among all anions, anion with highest ionic conductance is OH−
\lambda_{OH^{-}}^\infty = 197.8 ohm−1 cm2 mole−1
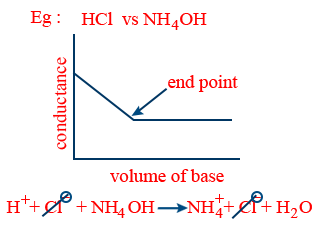
(i) Strong acid vs strong base: 
- (ii) Strong acid vs weak base:
- (iii) (a) weak acid vs strong base:
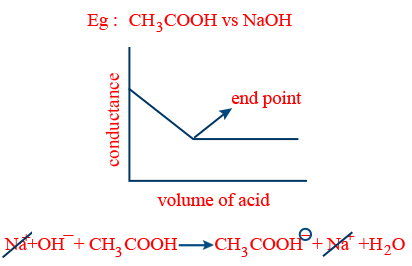
- (b) weak acid vs strong base:
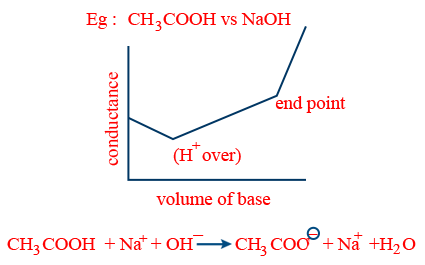
- (iv) weak acid vs weak base:
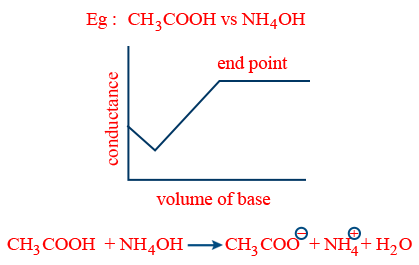
- (v) (strong acid + weak acid) vs strong base:
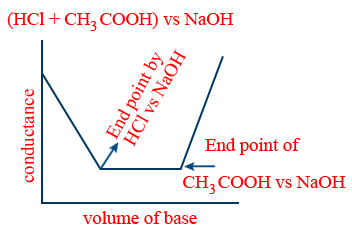
- Advantages of conductometric titration:
(i) Colored solution can be titrated.
(ii) End point of weak acid vs weak base can be determined.
(iii) More accurate values are obtained.
Part1: View the Topic in this Video from 27:11 to 59:33
Part2: View the Topic in this Video from 0:40 to 29:33
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Kohlrausch's Law:
\tt \wedge_{eq}^{0}=\wedge_{A^{+}}^{0}+\wedge_{B^{-}}^{0}
(where, \tt \wedge_{A^{+}}^{0}\ and\ \wedge_{B^{-}}^{0} are the limiting molar conductivity of the cation and anion respectively).
2. Degree of dissociation (α)
\tt \alpha =\frac{molar\ conductance\ at\ concentration\ 'C'}{molar\ conductance\ at\ infinite\ dilution}=\frac{\wedge_m^C}{\wedge_m^\infty}
3. Dissociation constant \tt K_{c}=\frac{C\alpha^2}{1-\alpha}
4. \tt \wedge_m^0=\frac{k\times 1000}{solubility\left(in\ mol\ L^{-1}\right)}
5. Molar Conductivity (Λm)
\tt \wedge_m=\frac{k\times1000}{M} where, M = molarity. Its units are Ω-1 cm2 mol-1 or S cm2 mol-1
6. Debye-Huckel Onsagar equation
\tt \wedge_m=\wedge_m^0-A\sqrt{C}
where, A is a constant.

