Chemical Kinetics
Effect of Temperature and Catalyst, Activation Energy, Arrhenius Equation, Collision Theory
Effect of temperature on rate of reaction:
Every increase in temperature by 10°, increases the collision frequency only by about 2% but the rate constant and the rate of reaction become double and in some cases triple.
Temperature coefficient (μ)=\tt \frac{K_{\left(t+10\right)}}{k_t} = 2
(i) Final rate = Initial rate \tt \left(\mu\right)^{\frac{\Delta T}{10}}
(ii) \tt \frac{k_{final}}{k_{initial}}=\left(\mu\right)^{\frac{\Delta T}{10}}
1. The reacting molecules should possess certain minimum energy for their activation, effective collision and product formation. This energy state is called threshold energy (or) energy barrier.
2. Arrhenius gave a relation between rate constant k, activation energy Ea, and temperature T in the form of an equation popularly known as Arrhenius equation. Fraction of molecules \tt \frac{n}{N} having energy equal or more than activation as energy is given by
\tt \frac{n}{N}=\frac{k}{A}=e^{-Ea/RT}
\tt k=A\cdot e^{\frac{-Ea}{RT}}
A is Arrhenius frequency factor (or) pre exponential factor, R is molar gas constant.
e-Ea/RT is the fraction of total molecules "N" possessing energy equal or more than threshold energy known as Boltzmann factor.
3. T cannot be extremely high. This will give k = A. i.e, all collisions will produce products, which is impossible.
4. Ea cannot be zero. This will give k = A i.e. all collisions will produce products, which is impossible.
5. Ea cannot be negative. It will mean \tt k=A\cdot e^{+\frac{Ea}{RT}}=A\left(1+\frac{Ea}{RT}\right) i.e, k>>A, which is impossible.
6. \tt \log k=\frac{-Ea}{2.303\ R}\frac{1}{T}+\log\ A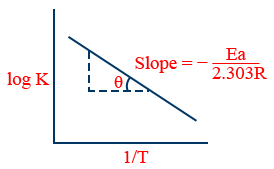
7. At two different temperatures \tt \log \frac{k_2}{k_1}=\frac{Ea}{2.303\ R}\left[\frac{1}{T_1}-\frac{1}{T_2}\right]
Effect of catalyst on the rate of reaction:
(i) It should be clearly kept in mind that energy of reaction, extent of reaction and ΔG value for the reaction do not change at all by the use of catalyst.
(ii) If kc and k are rate constants with and without catalysts, according to Arrhenius equation, we have
\tt \frac{k_c}{k}=e^{\left(E-E_C\right)/RT}=e^{\Delta E/RT}
\tt \Delta E=2.303\ RT\ \log \frac{k_c}{k}
Collision theory:
(i) The number of collisions per unit volume per second of the reaction mixture is called as collision frequency(Z).
(ii) If the probability or steric factor (proper orientation factor) to account for effective collision is 'P' the rate of reaction is given by
\tt Rate=P\ Z\ e^{\frac{-Ea}{RT}}
(iii) The main drawback of this theory is that it considers atoms and molecules as hard spheres.
Tricks
(i) Higher the value of Ea, slower is the reaction because the fraction of molecules having energy equal to or more than threshold energy will be quite less.
(ii) Order of a single step reaction is always equal to its molecularities.
(iii) Enzymatic reactions have lower activation energy than metal catalyzed reactions and hence are much faster.
(iv) For a hypothetical reaction
\tt aA+bB \longrightarrow cC
\tt -\frac{1}{a}\frac{\Delta \left[A\right]}{\Delta t}= -\frac{1}{b}\frac{\Delta \left[B\right]}{\Delta t}= +\frac{1}{c}\frac{\Delta \left[C\right]}{\Delta t} = rate of reaction
(v) Parallel reactions those follows 1st order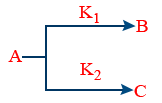
\tt rate\ -\frac{d\left[A\right]}{dt}=k_1\left[A\right]+k_2\left[A\right]=\left(k_1+k_2\right)\left[A\right]
(a) \tt B%=\frac{k_1}{K_1+k_2}\times 100\%
\tt C%=\frac{k_2}{K_1+k_2}\times 100\%
(vi) For a reversible reaction 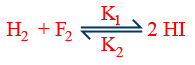
rate w.r.t \tt HI=\frac{1}{2}\frac{\Delta \left[HI\right]}{\Delta t}=k_2\left[H_2\right]\left[I_2\right]-k_2\left[HI\right]^2
Net rate of formation of \tt HI=\frac{\Delta \left[HI\right]}{\Delta t}=2K_1\left[H_2\right]\left[I_2\right]-2k_2\left[HI\right]^2
(vii) Rate of very fast reactions are studied by spectro photometry.
(iii) For parallel reaction
\tt E_a=\frac{k_1E_{a_1}+k_2Ea_2}{k_1+k_2}
For nth order reaction
\tt k.t=\frac{1}{n-1}\left[\frac{1}{\left[A\right]^{n-1}}-\frac{1}{\left[A\right]^{n-1}_0}\right] [n should not be 1]
(x) For nth order reaction
\tt t_{1/2}=\frac{1}{k\left(n-1\right)}\frac{2^{n-1}-1}{\left[A\right]^{n-1}_{0}}
Part1: View the Topic in this Video from 0:08 to 18:12
Part2: View the Topic in this Video from 0:08 to 7:18
Part3: View the Topic in this Video from 0:08 to 10:12
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Ea = E(Threshold energy) E(Reactants)
Activation energy = Threshold energy − Average kinetic energy of the reacting molecules.
2. \tt \log\ k=\log\ A-\frac{E_{a}}{2.303RT}

