Work, Energy and Power
Power and Collisions
- Power is the rate of doing work.
- \tt P = \frac{w}{t} (or) \tt P = \frac{dw}{dt}
- Power is a scalar quantity.
- Power P = Force · Velocity = \tt \overline{F} \cdot \overline{V}
- Erg/Sec is the CGS unit of power.
- Walt is the MKS unit of power.
- Average power \tt P_{avg} = \frac{w}{t} = \frac{\frac{1}{2} mv^{2}}{t} = \frac{F \cdot V}{2}
- If a particle moves with constant velocity Pavg = Pinst
- Power of machine gun \tt P = \frac{1}{2} \frac{mnv^{2}}{t}
- Conveyor belt is moving with velocity ‘v’ Gravel is poured at \tt \frac{dm}{dt} rate \tt P = \left(\frac{dm}{dt}\right) v^{2}
- Power of a motor to throw water of density ‘ρ’ with velocity ‘v’ from a tube of area of crossection ‘A’ is P = A ρv3.
- Power of a motor to lift water of mass ‘m’ to a height ‘h’ in time ‘t’ and pumps with velocity V.
\tt P = \frac{mgh + \frac{1}{2} mv^{2}}{t} - Power of car engine P = (R + ma) v {R = Resistance offered}.
- To get ‘n’ times of water force must be increased by n2 times F1 = n2F.
- To get ‘n’ times of water power must be increased by n3 times P1 = n3P.
- When power of engine is constant velocity \tt V \propto t^{\frac{1}{2}}.
- When power of engine is constant displacement \tt S \propto t^{\frac{3}{2}}.
- 1 watt = \tt \frac{1 Joule}{1 sec}
- 1 Horse power = 746 watt.
- 1 Kilo watt hour = 3.6 × 106 Joules.
- Efficiency \tt \eta = \frac{Power \ output}{Power \ input}
- Gravitational potential energy \tt U = \frac{mgh}{\left(1 + h/R\right)}
- Electrical potential energy \tt U = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{1}q_{2}}{r}
- Block is pulled by a constant power over a surface with coefficient of friction (μ). The velocity V = \frac{P}{\mu mg}.
- Power can also be represented as P = Fv cos θ.
- A collision is a redistribution of momenta ignoring the effect of other forces with or without physical interaction.
- In a collision there need not be a physical contact between two entities.
- A elastic collision is that in which both momentum and kinetic energy are conserved.
- Collision between sub atomic particles is the example for elastic collision.
- An inelastic collision is that in which only momentum is conserved and not the kinetic energy.
- Collision between automobiles is an example for inelastic collision.
- A collision which takes place along a straight line is called Head on (or) one dimensional collision.
- A oblique collision is that in which before and after the collision are not along the same line.
- Coefficient of restitution (e) is defined as the ratio of relative velocity of separation after collision to relative velocity of approach before collision.
- Coefficient of restitution (e) is a pure number.
- Coefficient of restitution (e) has no units and dimensions.
- Coefficient of restitution (e) is termed as degree of elasticity.
- Practically "e" lies between 0 and 1.
- For perfectly elastic collision e = 1.
- For perfectly inelastic collision e = 0.
- For semi elastic collision 0 < e < 1.
- The value of ‘e’ depends upon nature of colliding bodies.
- When a body is dropped from ‘h1’ (or) bounces to height ‘h2’ \tt e = \sqrt{\frac{h_{2}}{h_{1}}}
- Height after nth bounce hn = e2n h0.
- If a body incidents with velocity "v" and bounces back with velocity v'. \tt e = \frac{V^{'}}{V}
- If a body takes a time ‘t’ to travel and ‘t'’ to bounce back \tt e = \frac{t^{'}}{t}.
- Time taken for nth bounce tn = en · t.
- Velocity after nth bounce vn = en · v.
- If a ball takes ‘n’ bounces then total distance travelled \tt d = H \left(\frac{1+e^{2}}{1-e^{2}}\right).
- If a ball takes ‘n’ bounces then total time takes to travel \tt T = \sqrt{\frac{2H}{g}} \left(\frac{1+e}{1-e}\right).
- Average speed for ‘n’ bounces = \tt \frac{H \left(\frac{1+e^{2}}{1-e^{2}}\right)}{\sqrt{\frac{2+1}{g}}\left(\frac{1+e}{1-e}\right)}.
- Average velocity for ‘n’ bounces = \tt \frac{H}{\sqrt{\frac{2H}{g}} \left(\frac{1+e}{1-e}\right)}.
- Final velocity of first body after one dimensional elastic collision \tt V_{1} = \left(\frac{m_{1}-m_{2}}{m_{1} + m_{2}}\right) u_{1} + \frac{2 m_{2}u_{2}}{m_{1} + m_{2}}.
- For second body \tt V_{2} = \frac{m_{2}-m_{1}}{m_{1} + m_{2}} \left(u_{2}\right) + \frac{2 m_{1}u_{1}}{m_{1} + m_{2}}.
- Loss in kinetic energy = \tt \frac{1}{2} \frac{m_{1}m_{2}}{m_{1} + m_{2}} \left(u_{1} - u_{2}\right)^{2} = 0 in elastic collision.
- Common velocity of compound body after perfectly inelastic collision is \tt V = \frac{m_{1}u_{1} + m_{2}u_{2}}{m_{1} + m_{2}}.
- Loss in KE in elastic collision = \tt \frac{1}{2} \frac{m_{1}m_{2}}{m_{1} + m_{2}} \left(u_{1} - u_{2}\right)^{2}.
- Final velocity for semi elastic collision. \tt V_{1} = \left(\frac{m_{1} - em_{2}}{m_{1} + m_{2}}\right) u_{1} + \left(\frac{1+e}{m_{1} + m_{2}}\right) m_{2}u_{2}.
- \tt V_{2} = \left(\frac{m_{e} - em_{1}}{m_{1} + m_{2}}\right) u_{2} + \left(\frac{1+e}{m_{1} + m_{2}}\right) m_{1}u_{1}
- Loss in KE in semi elastic collision. \tt \frac{1}{2} \left(\frac{m_{1} m_{2}}{m_{1} + m_{2}}\right) \left(1-e^{2}\right) \left(u_{1} - u_{2}\right)^{2}.
- In perfectly inelastic collision the ratio of loss of energy of the system and its initial energy if u2 = 0 \tt \frac{\Delta KE}{Ei}= \frac{m_{2}}{m_{1} + m_{2}}.
- In perfectly inelastic collision the ratio of final energy to initial energy \tt \frac{Ef}{Ei} = \frac{m_{1}}{m_{1} + m_{2}}.
- In elastic collision ‘m2’ is at rest KE of m1 before collision is E then kinetic energy of m1 after collision \tt K_{1} = \left(\frac{m_{1} - m_{2}}{m_{1} + m_{2}}\right)^{2} E.
- In elastic collision ‘m2’ is at rest and KE of m1 before collision is E then kinetic energy of m2 after collision \tt K_{2} = \frac{4m_{1}m_{2}}{\left(m_{1} + m_{2}\right)^{2}} E.
- In the above case fraction of KE retained by "m1" is \tt \left(\frac{m_{1} - m_{2}}{m_{1} + m_{2}}\right)^{2}.
- Fraction of KE retained by m2= \tt \frac{4m_1m_2}{\left(m_{1} + m_{2}\right)^{2}}.
- If target particle is very light v1 = u1 & v2 = 2u1 (u2 = 0).
- Velocity of bullet from Ballistic pendulum \tt V_{bullet} = \frac{\mu + m}{m} \sqrt{2gh}.
- For oblique impact of smooth spheres.
v1 sin θ1 = u1 sin α1
v2 sin θ2 = u2 sin α2 - m1v1 cos θ1 + m2v2 cos θ2 = m1u1 cos α1 + m2u2 cos α2
- \tt e = \frac{\left(v_{2} \cos \theta_{2} - v_{1} \cos \theta_{1}\right)}{\left(u_{1} \cos \alpha_{1} - u_{2} \cos \alpha_{2}\right)}.
- \tt V_{1} \cos \theta_{1} = \frac{\left(m_{1} - em_{2}\right) u_{1} \cos \alpha_{1} + \left(1 + e\right) m_{2} u_{2} \cos \alpha}{\left(m_{1} + m_{2}\right)}.
- \tt V_{2} \cos \theta_{2} = \frac{\left(1 + e\right) m_{1}u_{1} \cos \alpha_{1} + \left(m_{2} - em_{1}\right) u_{2} \cos \alpha_{2}}{\left(m_{1} + m_{2}\right)}.
- \tt \Delta KE=\frac{1}{2} \frac{m_{1} m_{2}}{m_{1} + m_{2}} \left(1 - e^{2}\right) \left(u_{1} \cos \alpha_{1} - u_{2} \cos \alpha_{2}\right)^{2}.
- Collision between blocks with spring \tt E = \frac{1}{2} m_{1}{u_{1}^{2}} + = \frac{1}{2} m_{2}{u_{2}^{2}} + \frac{1}{2} Kx^{2}
- Change in momentum along Normal to spheres = m(v cos α + u cos θ) = m (1 + e) u cos θ.
- Momentum principle in collision.\tt P^{2} = P_{1}^{2} + P_{2}^{2} + 2P_{1}P_{2} \cos \theta.
- Two particles m1 & m2 attached to a string on either ends or an impulse J is given as shown. Then final velocity of m2
\tt V_{2} = \frac{J \cos \theta}{m_{1} + m_{2}}.
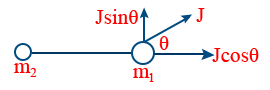
- Final velocity of m1 \tt V_{1} = \frac{J \sin \theta}{m_{1}}.
View the Topic in this video From 0:55 To 57:44
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Average power (Pav.) = \tt \frac{\Delta W}{\Delta t}=\frac{W}{t}
2. Instantaneous power (Pinst.) = \tt \frac{dW}{dt}=\frac{\overrightarrow{F}.d\overrightarrow{s}}{dt}
Pinst = \overrightarrow{F}.\overrightarrow{v}
3. Inelastic one Dimensional collision
Velocities after collision v_{1}=\frac{\left(m_{1}-m_{2}\right)u_{1}+2 m_{2}u_{2}}{\left(m_{1}+m_{2}\right)}\ and\ v_{2}=\frac{\left(m_{2}-m_{1}\right)u_{2}+2 m_{1}u_{1}}{\left(m_{1}+m_{2}\right)}
4. Loss of kinetic energy \tt \Delta E= \frac{m_{1}m_{2}}{2\left(m_{1}+m_{2}\right)}\left(u_{1}-u_{2}\right)^2\left(1-e^{2}\right)
5. In perfectly Inelastic one Dimensional collision : Velocity of separation after collision = 0
Loss of kinetic energy = \tt \frac{m_{1}m_{2}\left(u_{1}-u_{2}\right)^2}{2\left(m_{1}+m_{2}\right)}
6. If a body is dropped from a height h0 and it strikes the ground with velocity v0 and after inelastic collision it rebounds with velocity v1 and rises to a height h1, then
e=\frac{v_{1}}{v_{0}}=\sqrt{\frac{2gh_{1}}{2gh_{0}}}=\sqrt{\frac{h_{1}}{h_{0}}}
7. If after n collisions with the ground, the body rebounds with a velocity vn and rises to a height hn, then
e^{n}=\frac{v_{n}}{v_{0}}=\sqrt{\frac{h_{n}}{h_{0}}}
8. Two Dimensional or Oblique collision: In horizontal direction, m_{1}u_{1}\cos\alpha_{1}+m_{2}u_{2}\cos\alpha_{2}=m_{1}v_{1}\cos\beta_{1}+m_{2}v_{2}\cos\beta_{2}
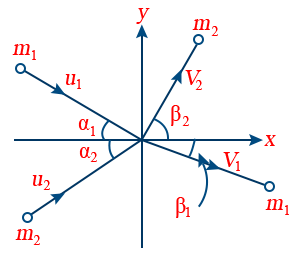
9. In vertical direction, m_{1}u_{1}\sin\alpha_{1}-m_{2}u_{2}\sin\alpha_{2}=m_{1}v_{1}\sin\beta_{1}+m_{2}v_{2}\sin\beta_{2}
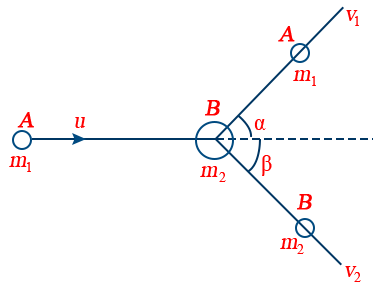
10. Perfectly Inelastic collision:
When the colliding bodies are moving in the same direction
Loss in kinetic energy \Delta K=\frac{1}{2}\left(\frac{m_{1}m_{2}}{m_{1}+m_{2}}\right)\left(u_{1}-u_{2}\right)^2
11. When the colliding bodies are moving in the opposite direction
Loss in kinetic energy = \frac{1}{2}\ \frac{m_{1}m_{2}}{m_{1}+m_{2}}\ \left(u_{1}-u_{2}\right)^2
12. Velocity of block after collision: v=\frac{mu}{\left(m+M\right)}
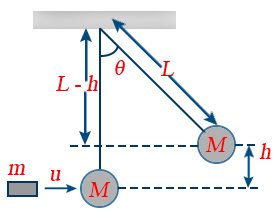
13. Velocity of bullet after collision: u=\left[\frac{\left(m+M\right)\sqrt{2gh}}{m}\right]
14. Loss in kinetic energy \Delta K=\frac{1}{2}\ \frac{mM}{m+M}\ u^{2}
15. Angle of string from the vertical \theta=\cos^{-1}\left[1-\frac{1}{2gL}\left(\frac{mu}{m+M}\right)^2\right]

