System of Particles and Rotational Motion
Moment of Inertia
- Moment of inertia is the inability of a body to change its state of rotation.
- Moment of inertia is the rotational inertia.
- Moment of inertia is a scalar quantity.
- unit of moment of inertia is kg m2.
- Moment of inertia of a particle of mass ‘m’ at a distance ‘s’ is I = mr2.
- Moment of inertia of a group of system of particles \tt I=m_{1}r_1^2+m_{2}r_2^2+...m_{n}\ r_{n}^{2}
- For system of particles \tt I=\Sigma\ mr^{2}.
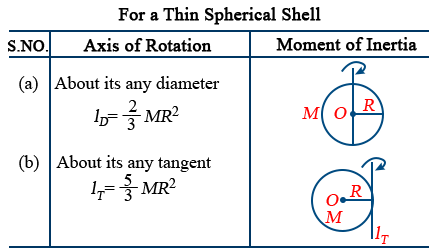
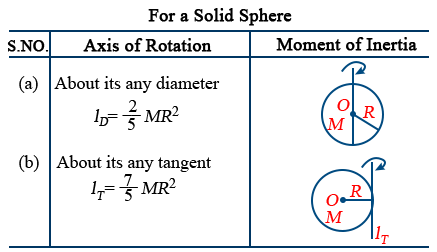
- For a rigid body I = MK2.
- Radium of gyration \tt K=\sqrt{\frac{r_1^2+r_2^2...r_n^2}{n}}.
- Moment of inertia of a body depends on mass of the body
- Moment of inertia of a body depends on distribution of mass of the body
- Moment of inertia of a body depends on position of axis of rotation.
- Moment of inertia is independent of angular velocity of rotation of the body
- Radius of gyration of a body depends on distribution of mass and position of axis of rotation.
- Radian of generation is independent of mass of rotating body.
- Parallel axes theorem I = Ic + Md2 d = perpendicular distance of parallel axes.
- Parallel axes theorem \tt K=k_1^2+d^{2}
- Perpendicular axes theorem IZ = Ix + Iy
- Perpendicular axes there \tt KZ^{2}=k_x^2+k_y^{2}
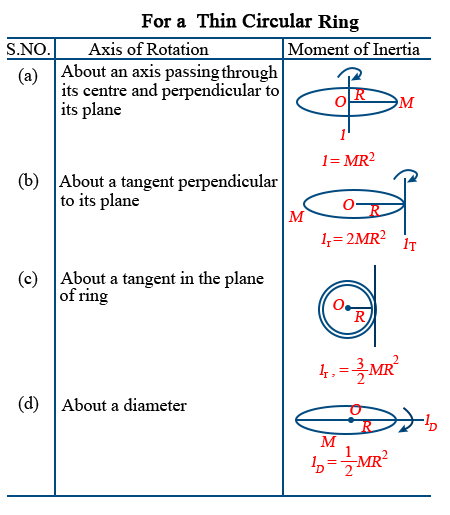
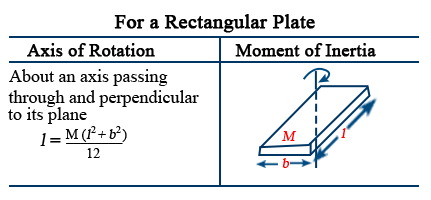
- Moment of inertia of circular ring axis passing
- Through centre and normal to its plane I = MR2.
- Work done by torque w = Tθ
- Work energy principle \tt \omega=\frac{1}{2}\ I\ \left(\omega_2^2-\omega_1^2\right)
- Power of a torque \tt P=\frac{d\omega}{dt}=\tau\frac{d\theta}{dt}=\tau\omega.
-
Velocity at lower point \tt \overline{V}_{p}=\overline{V}_{pc}+\overline{V}_{c}
- In pure rolling Vc = Vpc = V ⇒ Vp = 0
\tt V_{p}=\sqrt{Vpc^{2}+Vc^{2}+2Vpc\ Vc \cos\theta} - Kinetic Energy translation of pure rolling =\tt \frac{1}{2}\ Mv^{2}
- Kinetic Energy Rotational of pure rolling = \tt \frac{1}{2}\ I\omega^{2}
- Kinetic Energy Rotational of pure rolling = \tt \frac{1}{2}MK^{2}\ \frac{V^{2}}{R^{2}}=\frac{1}{2}\ MV^{2}\left(\frac{K^{2}}{R^{2}}\right)
- Kinetic Energy total = KEtrans + KErot
- Kinetic Energy trans = \tt \frac{1}{2}MV^{2}+\frac{1}{2}\ MV^{2}\left(\frac{K^{2}}{R^{2}}\right)
- Kinetic Energy trans = \tt \frac{1}{2}MV^{2}\left(1+\frac{K^{2}}{R^{2}}\right).
- Fraction of translational \tt KE=\frac{1}{1+\frac{K^{2}}{R^{2}}}=\frac{R^{2}}{R^{2}+K^{2}}.
- Fraction of rotational \tt KE=\frac{1}{1+\frac{R^{2}}{K^{2}}}=\frac{K^{2}}{R^{2}+K^{2}}.
- In the case of rolling bodies KE translation ≥ KE rotaion.
- In the case of rolling circular ring or rolling hollow cylinder KE trans = KE rotation.
- Rolling body Acceleration down an incline \tt a=\frac{Mg\sin \theta-f}{M}.
- Rolling body Acceleration down an incline \tt a=\frac{g\sin \theta}{1+I/\ MR^{2}}.
- Coefficient of friction \tt \mu\ \geq\frac{\tan\theta}{1+\frac{MR^{2}}{I}}
- Velocity acquired by rolling body on incline \tt V=\sqrt{\frac{2gh}{1+\frac{K^{2}}{r^{2}}}}.
- Time taken by the body rolling down an incline \tt t=\frac{1}{\sin \theta}\ \sqrt{\frac{2h}{g}\left(1+\frac{K^{2}}{r^{2}}\right)}
- Frictional force = \tt \frac{mg \sin\theta}{1+\frac{r^{2}}{k^{2}}}
View the Topic in this video From 02:38 To 54:19
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.