System of Particles and Rotational Motion
Centre of Mass and Its Motion
- Centre of mass of a body or system of particles is the point at which the whole mass of the body (or) system supposed to be concentrated.
- The motion of centre of mass represents the motion of the whole body
- There may or may not be mass at centre of mass
- Centre of mass is an imaginary point
- The moments about the centre of mass is same m1x1 = m2x2
- The centre of mass of heavier and lighter mass system the centre of mass lies nearer to the heavier mass.
- \tt X_{cm}=\frac{m_{1}x_{1}+m_{2}x_{2}+...+\ m_{n}x_{n}}{m_{1}+m_{2}+...+\ m_{n}}
- \tt Y_{cm}=\frac{m_{1}y_{1}+m_{2}y_{2}+...+\ m_{n}y_{n}}{m_{1}+m_{2}+...+\ m_{n}}
- \tt Z_{cm}=\frac{m_{1}z_{1}+m_{2}z_{2}+...+\ m_{n}z_{n}}{m_{1}+m_{2}+...+\ m_{n}}
- \tt r_{cm}=\frac{m_{1}r_{1}+m_{2}r_{2}+...+\ m_{n}r_{n}}{m_{1}+m_{2}+...+\ m_{n}}
- Relative to centre of mass \tt m_{1}\overline{r_{1}}+m_{2}\overline{r_{2}}+...+m_{n}\overline{r_{n}}=0
- For Continuous mass distribution \tt X_{cm}=\frac{\int x\ dm }{\int dm}
- For Continuous mass distribution \tt Y_{cm}=\frac{\int y\ dm }{\int dm}
- For Continuous mass distribution \tt Z_{cm}=\frac{\int z\ dm }{\int dm}
- For Uniform shaped and regular bodies centre of mass lies at their Geometric centre.
- For Non uniform and irregular shaped bodies centre of mass lies outside the body.
- Two circular dices of radii “r1 and r2” of same material are kept in contact \tt X_{cm}=\frac{r_2^2\left(r_{1}+r_{2}\right)}{r_1^2+r_2^2}
- Two spheres of radii ‘r1’ and ‘r2’ of same material are kept in contact \tt X_{cm}=\frac{r_3^3\left(r_{1}+r_{2}\right) }{r_1^3+r_2^3}
- Two rods of length L1 and L2 joined as T shape. \tt X_{cm}=\frac{L_2^2}{2\left(L_{1}+L_{2}\right)}
- Two cylindrical rods kept in contact along their length \tt X_{cm} = \frac{r_2^2\ L_{2}}{\left(r_2^2\ L_{1}+r_2^2\ L_{2}\right)} \left[\frac{L_{1}+L_{2}}{2}\right]
- If Δx1, Δx2 are shift in positions of 1st and 2nd particles then \tt \Delta X_{cm}=\frac{\pm\ m_{1}\Delta\ x_{1}\pm\ m_{2}\Delta\ x_{2}}{m_{1}+m_{2}} + when shifted along +ve x direction − when shifted along –ve x direction
- Similarly \tt \Delta Y_{cm}=\frac{\pm\ m_{1}\Delta\ y_{1}\pm\ m_{2}\Delta\ y_{2}}{m_{1}+m_{2}}
- Velocity of centre of mass \tt V_{cm}=\frac{m_{1}\nu_{1}+\ m_{2}\nu_{2}+...+\ m_{n}\nu_{n}}{m_{1}+m_{2}+...+\ m_{n}}
- M Vcm = P1 + P2 + ---- + Pn {P1 = Momentum}
- Two particles moving perpendicular \tt V_{cm}=\sqrt{\frac{m_1^2 v_1^2+m_2^2 v_2^2}{\left(m_{1}+m_{2}\right)^{2}}}
- Acceleration of centre of mass = \tt a_{cm}=\frac{m_{1}a_{1}+\ m_{2}a_{2}\ +...+\ m_{n}a_{n}}{m_{1}+m_{2}+...+m_{n}}
- \tt M\ \overline{acm}=F\ external
- Centre of mass can be accelerated only by a net external force.
- Internal forces cannot accelerate centre of mass
- In absence of external forces velocity of cm = O
- Shift in centre of mass when a small portion of mass is removed \tt x\ shift=\frac{m_{removed}}{m_{total}-m_{removed}}
- When a circular disc or radius ‘r’ is removed from a circular disc or radius ‘R’. \tt Shift=\frac{r^{2}d}{R^{2}-r^{2}}
- If a circular portion of diameter “R” is removed from a circular disc of radius R. X shift = \tt \frac{R}{6}
- If centre of removed plate and original plate coincide then shift is zero.
- When a sphere of radius ‘r is removed from a sphere of radius R, \tt Shift=\frac{r^{3}d}{R^{3}-r^{3}}
- When a triangular portion is removed from a square plate of side ‘a’. \tt X_{shift}=\frac{a}{9}
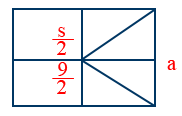
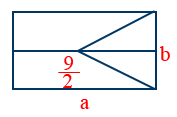
- For a rectangular plate \tt X_{shift}=\frac{a}{9}
- When & shell in flight Explodes acm = g downwards.
- The centre of mass of all fragments will continue to move along the same tragatery as fragments in space.
- A man of mass ‘m’ walks a distance ‘L’ on the boat & boat is displaced in opposite direction \tt X=\frac{mL}{M+m}.
- Distance walked by the man relative to shore (or) water is (L – X).
- When two masses more under mutual force of attraction towards each other \tt \overline{V}_{cm}=0\ and\ \overline{a}_{cm}=0
- \tt m_{1}\overline{v}_{1}=-m_{2}\overline{v}_{2} ( F Ext=0)
\tt m_{1}\overline{a}_{1}=-m_{2}\overline{a}_{2} ( F Ext=0) - Papper’s 1st Law volume V = 2π Xc × S ( S = Surface area)
- Papper’s 2nd Law Area S = 2π Xc × Πr
- Centre of mass of uniform rod = L/2.
- Centre of mass of semi circular ring = 2R/ π.
- Centre of mass of a semi circular disc of radius R from centre is 4R/3π.
- Centre of mass of a quadrant of a circle of radius R from centre is \tt 4R/\pi\sqrt{2}
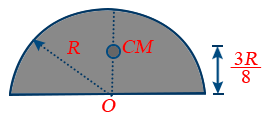
- Centre of mass of a solid semi sphere of radium ‘R’ from centre is 3R/8.
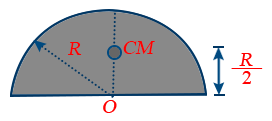
- Centre of mass of a hollow semi sphere of radium R is \tt \frac{R}{2}.
- Centre of mass of a solid cone is h/4 from base.
- Centre of mass of a hollow cone is h/3 from base.
- Centre of mass of a solid sphere is R from base.
View the Topic in this video From 0:50 To 50:03
View the Topic in this video From 01:39 To 53:11
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. The position of centre of mass from m_{1} = \frac{m_{2}d}{m_{1} + m_{2}}

2. Position of centre of mass from m_{2} = \frac{m_{1}d}{m_{1} + m_{2}}
3. If position vectors of particles of masses m1 and m2 are r1 and r2 respectively, then \tt r_{CM} = \frac{m_{1}r_{1} + m_{2}r_{2}}{m_{1} + m_{2}}
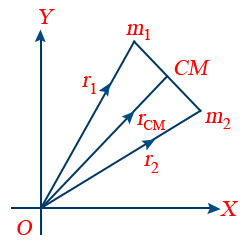
4. If in a two particle system, particles of masses m1 and m2 are moving with velocities v1 and v2 respectively, then velocity of the centre of mass \tt v_{CM} = \frac{m_{1}v_{1} + m_{2}v_{2}}{m_{1} + m_{2}}
5. If accelerations of the particles are a1and a2 respectively, then acceleration of the centre of mass \tt a_{CM} = \frac{m_{1}a_{1} + m_{2}a_{2}}{m_{1} + m_{2}}
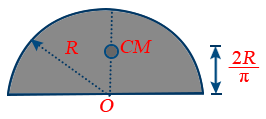
6. Centre of mass of a uniform semicircular ring of radius R lies at a distance of \tt h = \frac{2R}{\pi} from its centre; on the axis of symmetry as shown in the figure.
7. Centre of mass of a uniform semicircular disc of radius R lies at a distance of \tt h = \frac{4R}{3\pi} from the centre on the axis of symmetry as shown in figure.
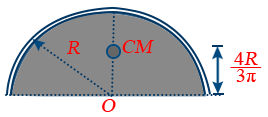
8. Centre of mass of a hemispherical shell of radius R lies at a distance of \tt h = \frac{R}{2} from its centre on the axis of symmetry as shown in figure.
9. Centre of mass of a solid hemisphere of radius R lies at a distance of \tt h = \frac{3R}{8} from its centre on the axis of symmetry as shown in the figure.
10. Velocity of centre of mass \tt \vec{v}_{CM} = \frac{m_{1}\vec{v}_{1} + m_{2}\vec{v}_{2} + .... + m_{N}\vec{v}_{N}}{m_{1} + m_{2} + .... + m_{N}} = \frac{\sum_{i = 1}^{N}m_{i}\vec{v}_{i}}{\sum_{i = 1}^{N}}m_{i} = \frac{\sum_{i = 1}^{N}m_{i}\vec{i}}{M}
11. Acceleration of centre of mass \tt \vec{a}_{CM} = \frac{m_{1}\vec{a}_{1} + m_{2}\vec{a}_{2} + .... + m_{N}\vec{a}_{N}}{m_{1} + m_{2} + .... + m_{N}} = \frac{\sum_{i = 1}^{N}m_{i}\vec{a}_{i}}{\sum_{i = 1}^{N}m_{i}} = \frac{\sum_{i = 1}^{N}m_{i}\vec{a}_{i}}{M}

