Motion in a Straight Line
Accelerated Motion
- Equations of motion are \tt s = ut+\frac{1}{2}at^{2}
v = u + at
v2 − u2 = 2as
\tt S_{n} = u + a\left(n-\frac{1}{2}\right) - Initial velocity of freely falling body is zero.
- Final velocity of freely falling body V = gt.
- Final velocity of freely falling body wr.to distance \tt v=\sqrt{2gh}
- Distance travelled in nth sec \tt S_{n}=0+g\left(n-\frac{1}{2}\right).
- Ratio of distances travelled in 1s , 2s , 3s .... = 1 : 4 : 9 : .......n2.
- Ratio of distances travelled in 1st 2nd 3rd = 1 : 3 : 5 .......(2n – 1).
- Body falls from height ‘h’ time of descent = \tt \sqrt{\frac{2h}{g}}
- For a vertically projected body The maximum height reached \tt H=\frac{u^{2}}{2g}
- Time of ascent \tt Ta=\sqrt{\frac{2H}{g}}=\frac{u}{g}
- Time of descent \tt Td=\sqrt{\frac{2H}{g}}=\frac{u}{g}
- Time of flight \tt Tf=2\sqrt{\frac{2H}{g}}=\frac{2u}{g}
- If as friction in considered ta < td.
- Body always travels g/2 m during last second of upward motion.
- Equation of motion of body projected from top as tower is =\tt H= -u \ t\ +\frac{1}{2}gt^{2}
- Velocity with which it striker \tt V=\sqrt{u^{2}+2gh}
- If a body is projected vertically up with ‘u’ from tower it reaches ground with velocity ‘nu’ \tt H=\frac{u^{2}}{2g}\left(n^{2}-1\right)
- A particle projected vertically up from top of tower “t1” sec to reach the ground another particle thrown down with same velocity takes “t2” sec velocity of projection \tt u=\frac{g}{2}\left(t_{1}-t_{2}\right). Height of tower \tt h=\frac{1}{2}g\ t_{1}t_{2}.
- For oblique projection Horizontal position with time x = u cos θ t.
- For oblique projection vertical position with time \tt y=u\sin\theta\ t-\frac{1}{2}\ gt^{2}
- Equation of trajectory Y = \tt \tan\theta x-\frac{g}{2u^{2}\cos ^{2}\theta}\ x^{2}
- Time of ascent \tt Ta=\frac{u\sin\theta}{g}
- Time of flight \tt Tf=\frac{2u\sin\theta}{g}
- Maximum Height \tt H=\frac{u^{2}\sin^{2}\theta}{2g}
- Range (Horizontal) \tt R=\frac{u^{2}\sin 2\theta}{g}
- Range is maximum when θ = 45° R =\tt \frac{u^{2}}{g}
- Velocity of projectile at any instant t \tt V=\sqrt{\left(u\cos\theta\right)^2+\left(u\sin\theta-gt\right)^{2}}
- Angle made by projectile with horizontal \tt Tan \ \alpha=\left(\frac{u\sin\theta-gt}{u\cos\theta}\right)
- Vertical component of velocity at half of maximum height = \tt \sqrt{\left(u\cos\theta\right)^{2}+\left(\frac{u\sin\theta}{\sqrt{2}}\right)^2}
- If the particle passes two points situated at same height h at t1 and t2 time Then time of flight T = t1 + t2 & \tt h=\frac{1}{2}g\ t_{1}t_{2}
- Angular momentum of particle at maximum height about point of projection \tt L=mu\ \cos\theta\times\frac{u^{2}\sin^{2}\theta}{2g}
- Torque acting on a particle at max height = \tt mg\times\frac{R}{2}.
- For complementary angles range is same.
- Let h1 and h2 are heights “T1” and “T2” time of flights \tt h_{1}+h_{2}=\frac{u^{2}}{2g}\ R=4\sqrt{h_{1}h_{2}}\ R=\frac{1}{2}\ g\ T_{1}T_{2}
- Time of flight of oblique projection from inclined plane \tt T=\frac{2u\sin\left(\alpha-\beta\right)}{g\cos \beta}
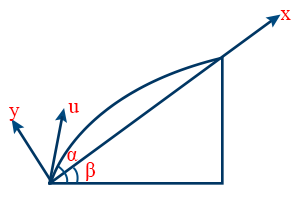
- Range \tt R=\frac{u^{2}}{g\cos^{2}\beta}\left[sin\left(2\alpha-\beta\right)-\sin\beta\right]
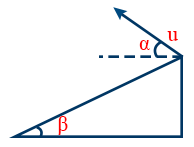
- Time of flight of projectile thrown down the inclined plane \tt T=\frac{2u\sin\left(\alpha+\beta\right)}{g\cos \beta}
- Range down the plane \tt R=\frac{2u^{2}\cos\alpha\ sin\left(\alpha+\beta\right)}{g\cos^{2}\beta}
- Horizontal position of horizontal projectile X = ut
- Vertical position of horizontal projectile \tt y=\frac{1}{2}gt^{2}.
- Equation of projector of horizontal projectile \tt y=\frac{gx^{2}}{2u^{2}}
- Time of descent of horizontal projection \tt t=\sqrt{\frac{2h}{g}}
- Range of horizontal projection \tt R=u\sqrt{\frac{2h}{g}}
- Velocity of horizontal projectile at any instant \tt v=\sqrt{u^{2}+g^{2}t^{2}}
- Angle made by horizontal projectile after same time Tan α= \tt \frac{gt}{u}
- Velocity on reaching the ground \tt v=\sqrt{u^{2}+2gh}
- From a certain height if two bodies are projected horizontally with velocities ‘u1’ and ‘u2’ in opposite direction then time after which their velocity vectors one perpendicular \tt t=\sqrt{\frac{u_{1}u_{2}}{g}}
- Distance between the two bodies when their velocities are perpendicular \tt d=\sqrt{\frac{u_{1}u_{2}}{g}}(u1+u2)
- Time after which their displacement vectors are perpendicular \tt 2\sqrt{\frac{u_{1}u_{2}}{g}}
- Distance between then when their displacement vectors are perpendicular \tt 2 \sqrt{\frac{u_{1}u_{2}}{g}}(u1+u2)
- If a body covers equal distances in equal time intervals the motion is said to be uniform.
- If a body covers unequal distances in equal time intervals the motion is said to be non uniform.
- Equation of trajectory of oblique projection from top of a tower. \tt H=-u\sin\theta\ T\ +\frac{1}{2}gT^{2}
- Range in the above case R = (u cos θ)T.
- At maximum height of oblique projective angle between velocity and acceleration is 90°.
- At maximum height of oblique projection from tower angle between velocity and acceleration is 90° .
View the Topic in this video From 01:17 To 54:38
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Acceleration (a) = \tt \frac{Change\ in\ velocity\left(\Delta \nu\right)}{Time\ interval \left(\Delta t\right)}
2. Average acceleration : \tt \overrightarrow{a}_{a\nu}=\frac{\Delta\overrightarrow{\nu}}{\Delta t}=\frac{\overrightarrow{\nu}_{2}-\overrightarrow{\nu}_{1}}{\Delta t}
3. Instantaneous acceleration : \tt \overrightarrow{a}=\lim_{\Delta t \rightarrow 0}\frac{\Delta \overrightarrow{\nu}}{\Delta t}=\frac{d\overrightarrow{\nu}}{dt}
4. Equations of Uniformly Accelerated Motion:
(i) v = u + at (ii) \tt s=ut+\frac{1}{2}at^{2} (iii) v2 = u2 + 2as
5. Distance travelled in nth second \tt S_{n}=u+\frac{a}{2}\left(2n-1\right)
6. If a body moves with uniform acceleration and velocity changes from u to v in a time interval, then the velocity at the mid point of its path = \tt \frac{\sqrt{u^{2}+\nu^{2}}}{2}

