Statistics
Measures of Dispersion
-
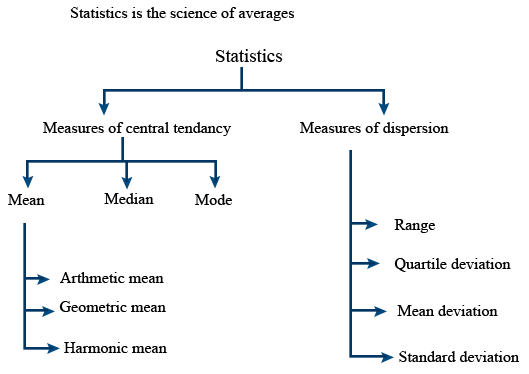
-
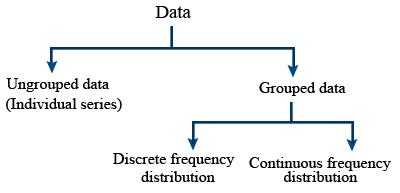
- If x1, x2, x3 ....... xn are the n values of x then its arithmetic mean
\overline{x} = \frac{\sum x_i}{n} - If x1, x2, x3 ....... xn are the n values of x then its arithmetic mean
\overline{x} = A + \frac{\sum (x_i-A}{n})
where A is Assumed mean - If x1, x2, ....... xn are the n values of x and its corresponding frequencies are f1, f2, ...... fn, then its arithmetic mean
\tt \overline{x} = \frac{\sum f_i \ x_i}{N}
where N = Σ fi - If x1, x2, ....... xn are the n values of x and its corresponding frequencies are f1, f2, ...... fn, then its arithmetic mean
\tt \overline{x} = A + \frac{\sum f_i \ d_i}{N}
where di = xi −A
N = Σ fi
A = Assumed mean - If x1, x2, ....... xn are the n values of x and its corresponding sizes n1, n2, ...... nn, then its arithmetic mean is given by
\tt \overline{x} = \frac{\sum n_i \ x_i}{\sum n_i} - If x1, x2, ....... xn are the n values of x and its corresponding weights w1, w2, ...... wn, then its arithmetic mean is given by
\tt \overline{x} = \frac{\sum w_i \ x_i}{\sum w_i} - AM of (ax + b) = a AM (x) + b
= a\overline{x} + b - If x1, x2, ....... xn are the n values of x, then its geometric mean is
= \sqrt[n]{x_{1}. x_{2}. x_{3}......x_{n}} - GM = Anti log \left(\frac{\sum_{i = 1}^{n}\log (x_i)}{n}\right)
- If x1, x2, ....... xn are the mid values of n classes and its corresponding frequencies f1, f2, f3, ..... fn.
Then GM = \sqrt[N]{x_{1}^{f_{1}}, x_{2}^{f_{2}} ...... x_{n}^{f_{n}}}
where N = Σ fi - GM = Anti log \left(\frac{\sum_{i = 1}^{n} f_i \log (x_i)}{N}\right)
where N = Σ fi - If G1, G2, ....... Gn are the GM of the n series of sizes n1, n2, ...... nn, respectively. Then GM of the combined series is given by
\tt = \sqrt[N]{G_{1}^{n_{1}}, G_{2}^{n_{2}}, ...... G_{n}^{n_{n}}}
where N = n1 + n2 + ...... + nn - GM = Antilog \tt \left(\frac{\sum_{i = 1}^{n} n_i \ \log (G_i)}{N}\right)
where N = n1 + n2 + ...... + nn - If x1, x2, x3 ....... xn are the n values of x then Harmonic mean H.M = \tt \frac{n}{\frac{1}{x_{1}} + \frac{1}{x_{2}} + ..... + \frac{1}{x_{n}}}
- If x1, x2, ....... xn are the n values of x and its corresponding frequencies are f1, f2, ...... fn, then the Harmonic mean H.M = \tt \frac{\sum_{i = 1}^{n} f_i}{\sum_{i = 1}^{n} \frac{f_i}{x_i}}
- If all the numbers are equal, then A.M = G.M = H.M
- If the numbers are different A.M ≥ G.M ≥ H.M
- The relation between A.M, G.M, and H.M is (GM)2 = (AM)(HM)
- \tt velocity = \frac{distance}{time}
d1, d2, ....... dn are the distances, t1, t2, ....... tn are the times, v1, v2, ....... vn are velocities. Then average velocity = \tt \frac{d_{1} + d_{2} + ...... +d_{n}}{\frac{d_{1}}{v_{1}} + \frac{d_{2}}{v_{2}} + ..... +\frac{d_{n}}{v_{n}}} - If d1 = d2 = ....... = dn. Then the average velocity = \tt \frac{n}{\frac{1}{v_{1}} + \frac{1}{v_{2}} + ..... + \frac{1}{v_{n}}}
- If x1, x2, ....... xn are the n-observations. Then median = \tt \left(\frac{n + 1}{2}\right)^{th} observation, if n is odd
- If x1, x2, ....... xn are the n-observations. Then median = \tt \frac{1}{2}\left[\left(\frac{n}{2}\right)^{th} observation + \left(\frac{n}{2} + 1\right)^{th} observation\right]
- If x1, x2, x3 ....... xn are the n-values of x and its corresponding frequencies are f1, f2, ....... fn. Then median = \tt \left(\frac{N + 1}{2}\right)^{th} item, if N is odd
where N = Σ fi - If x1, x2, x3 ....... xn are the n-values of x and its corresponding frequencies are f1, f2, ....... fn. Then median = \tt \frac{1}{2}\left[\left(\frac{N}{2}\right)^{th} item + \left(\frac{N}{2} + 1\right)^{th} item\right]
where N = Σ fi - For Continuous frequency distribution, median = l + \left(\frac{\frac{N}{2} - F}{f} \times c\right)
l = lower bound
F = cumulative frequency just before the class
f = frequency of class
c = class size
Cumulative frequency just more than \frac{N}{2} is median class. - For individual series, quartile
Q_{t} = \left[\frac{t(n + 1)}{4}\right]^{th} observation - For individual series, decile D_{t} = \left[\frac{t(n + 1)}{10}\right]^{th} observation
- For individual series, persontile P_{t} = \left[\frac{t(n + 1)}{100}\right]^{th} observation
- For discrete series, Quartile Q_{t} = \left[\frac{t(N + 1)}{4}\right]^{th} item
- For discrete series decile D_{t} = \left[\frac{t(N + 1)}{10}\right]^{th} item
- For the discrete series, the persontile P_{t} = \left[\frac{t(N + 1)}{100}\right]^{th} item
- For the continuous series, the Quartile Q_{t} = l + \left(\frac{\frac{tN}{4} - F}{f} \times c\right)
- For the continuous series, the decile D_{t} = l + \left(\frac{\frac{tN}{10} - F}{f} \times c\right)
- For the continuous series, the Persontile is P_{t} = l + \left(\frac{\frac{tN}{100} - F}{f} \times c\right)
- For the individual series, the number is which is occured more number of times is considered as mode.
- For the discrete series, the variate which is having maximum frequency is considered mode
- For continuous series, the mode = l + \left(\frac{f_{m} - f_{1}}{2f_{m} - f_{1} - f_{2}} \times c\right)
l = lower limit
fm = Frequency of class
f1 = frequency preceding class
f2 = frequency succeeding class
c = class size - Mode = 3 Median − 2 Mean
- Mean − Mode = 3(Mean − Median)
- In Symmetric distribution, the upper and lower quartiles are equidistant from median
- For symmetric distribution median = Second Quartile (Q2) = 5th decile (D5) = 50th persontile (P50)
- The difference between the maximum and minimum items of the series is called range
- Coefficient of Range =\tt \frac{Range}{maximum + minimum}
- Quartile deviation = \tt \frac{Q_{3} - Q_{1}}{2}
- Coefficient of quartile deviation = \tt \frac{Q_{3} - Q_{1}}{Q_{3} + Q_{1}}
View the Topic in this video From 21:30 To 24:30
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.

