Conic Sections
Sections of a Cone, Circles
Tips:
- If we take the intersection of a plane with a cone, the section so obtained is called a conic section.
- When the plane cuts the double napped cone with different angles circle, ellipse, parabola and hyperbola are formed.
- ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a circle if h=0; a = b ≠ 0 and g2 + f2 – ac ≥ 0
- General equation of standard form of a circle is x2 + y2 + 2gx + 2fy + c = 0 if g2 + f2 – c > 0 then real circle, if g2 + f2 – c = 0 then point circle, if g2 + f2 – c < 0 then imaginary circle.
- The general equation of a circle is ax2 + ay2 + 2gx + 2fy + c = 0 its centre is \tt \left(\frac{-g}{a},\frac{-f}{a}\right) radius = \tt \frac{\sqrt{g^{2}+f^{2}-ac}}{\mid a\mid}
- The equation of the circle passing through origin and through the points of intersection of the line ax + by + c = 0 with co-ordinate axes is ab(x2 + y2) + c(bx + ay) = 0
- The equation of the circle with (x1 y1) and (x2 y2) a extremities of a diameter is (x - x1) (x - x2)+ (y – y1) (y – y2) = 0
- Any circle touching x-axis is of the form x2 + y2 +2gx + 2fy + g2 = 0. [c = g2] radius = |f|; if it is touching both axes then c = g2 = f2 and radius = |g| = |f|.
- Conditions for a line is tangent to a circle y = mx + c touches x2 + y2 = r2 is c2 = r2 (1 + m2)
- Suppose lx + my + n = 0 touches x2 + y2 = r2 then n2 = r2 (l2 + m2) and the point of contact is \tt \left(\frac{-lr^{2}}{n},\frac{-mr^{2}}{n}\right)
- Suppose lx + my + n = 0 touches x2 + y2 +2gx + 2fy + c = 0 is (l2 + m2) (g2 + f2 – c) = (lg + mf – n)2
- The equation of tangent to the circle x2 + y2 = r2 whose slope ‘m’ is \tt y = mx\ \pm\ r\sqrt{m^{2}+1}
- The intercept made by the circle x2 + y2 +2gx + 2fy + c = 0 on x-axis is \tt 2\sqrt{g^{2}-c}, on y-axis is \tt 2\sqrt{f^{2}-c}
- If 'r' is radius of a circle then a line which is at a distance ‘d’ from centre of the circle, cuts (a chord) an intercept of length \tt 2\sqrt{r^{2}-d^{2}}
- Equation of the tangent at ‘θ’ to the circle x2 + y2 = r2 is x cos θ + y sin θ = r
- Equation of the normal at ‘θ’ to the circle x2 + y2 = r2 is x sin θ – y cos θ = 0
- The equation of the normal at P(x1 y1) to x2 + y2 +2gx + 2fy + c = 0 is y1 (x + g) – x1 (y + f) = 0
- Equation of the chord joining the two points θ1 and θ2 of the circle x2 + y2 = r2 is \tt x \cos \left(\frac{\theta_{1}+\theta_{2}}{2}\right)+y \sin \left(\frac{\theta_{1}+\theta_{2}}{2}\right)= r \cos \left(\frac{\theta_{1}-\theta_{2}}{2}\right)
- The length of chord \tt \overline{AB} joining A(θ1), B(θ2) of the circle x2 + y2 = r2 (or) \tt \left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}= r^{2}\ is\ 2r \begin{vmatrix}\sin \frac{\left(\theta_{1}-\theta_{2}\right)}{2}\end{vmatrix}
- If 'C' is centre and ‘r’ is radius of a circle then the power of the point ‘P’ is defined as CP2 – r2
- Power of a point on the circle is zero, power is positive if point lies outside the circle power is negative if point lies inside the circle.
- If P(x1 y1) is a point lying outside of the circle S = 0 then the length of the tangent from ‘P’ is \tt \sqrt{S_{11}}
- If ‘P’ is a point (other than centre) in the plane of a circle and a secant line through ‘P’ cuts the circle in A and B. If the tangents at A and B intersect in Q, then the locus of ‘Q’ is a straight line called the polar of ‘P’ w.r.t the circle. ‘P’ is pole of the line.
- Pole of line lx + my + n = 0 w.r.t the circle x2 + y2 = r2 is \left(\frac{-lr^{2}}{n},\frac{-mr^{2}}{n}\right)
- The condition that the lines l1x + m1y + n1 = 0 and l2x + m2y + n2 = 0 to be conjugate w.r.t the circle x2 + y2 = r2 is r2 (l1 l2 + m1 m2 ) = n1 n2
- The condition that the lines l1x + m1y + n1 = 0 and l2x + m2y + n2 = 0 to be conjugate w.r.t the circle x2 + y2 + 2gx + 2fy + c = 0 is (g2 + f2 – c) (l1 l2 + m1 m2) = (l1 g + m1 f – n1) (l2 g + m2 f – n2)
- If 'c' is centre 'r' is radius of a circle and P, Q are a pair of inverse points then CP.CQ = r2
- The inverse point of (x1 y1) with respect to circle x2 + y2 = r2 is \tt \left[\frac{r^{2}x_{1}}{x_1^2+y_1^2}+\frac{r^{2}y_{1}}{x_1^2+y_1^2}\right]
- The inverse point of origin with respect to the circle x2 + y2 + 2gx + 2fy + c = 0 is \tt \left[\frac{-gc}{g^2+f^2}+\frac{-fc}{g^2+f^2}\right]
- Equation of the pair of tangents from origin to the circle x2 + y2 + 2gx + 2fy + c = 0 is (gx + fy)2 = c (x2 + y2)
- Area of the quadrilateral formed by the two tangents drawn from an external point to a circle and a pair of radii through their points of contact is \tt r\sqrt{S_{11}}
- The length of the chord of contact of the point P(x1 y1) w.r.t the circle S=0 is \tt 2r\sqrt{\frac{S_{11}}{S_{11}+r^{2}}}
- S=0 is a circle in standard form, with centre ‘c’ and radius r. If P(x1 y1) is a point then the area of the triangle formed by pair of tangents from ‘P’ and chord of contact of ‘P’ is \tt \frac {r{\left(S_{11}\right)^{3/2}}}{S_{11}+r^{2}}
- The locus of point of intersection of two tangents which include an angle ‘θ’ w.r.t the circle x2 + y2 = r2 is x2 + y2 = r2 cosec2 θ/2
- The locus of midpoints of chords of circle x2 + y2 = r2 which subtend angle ‘θ’ at centre is x2 + y2 = r2 cos2 θ/2
- Angle of intersection of ‘2’ circles is \tt \cos \theta\ = \frac{r_1^2+r_2^2-d^{2}}{2\ r_{1}r_{2}}
- Tricks
- The angle between the tangents from (α, β) to the circle x2 + y2 = a2 is \tt 2\ \tan^{-1}\left[\frac{a}{\sqrt{\alpha^{2}+\beta^{2}-a^{2}}}\right]
- If OA and OB are the tangents from the origin to the circle x2 + y2 + 2gx + 2fy + c = 0 and ‘c’ is the centre of the circle, then the area of the quadrilateral OACB is \tt \sqrt{c.\left(g^{2}+f^{2}-c\right)}
- The length of the common chord of the circles x2 + y2 + ax + by + c = 0 and x2 + y2 + bx + ay + c = 0 is \tt \sqrt{\frac{1}{2}\left(a+b\right)^{2}-4c}
- If 'O' is the origin and OP, OQ are tangents to the circle x2 + y2 + 2gx + 2fy + c = 0, then the circumcentre of the triangle OPQ is \tt \left(\frac{-g}{2},\frac{-f}{2}\right)
- The length of the chord intercepted by the circle x2 + y2 = r2 on the line \tt \frac{x}{a}+\frac{y}{b}=1\ is\ 2\sqrt{\left(\frac{r^{2}\left(a^{2}+b^{2}\right)-a^{2}b^{2}}{a^{2}+b^{2}}\right)}
- cos θ ∈ (-∝, -1) U (1, ∝) ⇒ circles do not intersect cos θ ∈ (-1, 1) ⇒ circles intersect each other cos θ = 0 ⇒ circles intersect each other orthogonally cos θ ∈ {-1, 1} ⇒ circles touch each other internally or externally
Introduction to Conic Sections
Introduction to Circle
Circle Examples
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. The general equation of a circle is given by x2 + y2 + 2gx + 2fy + c = 0, where centre fo the circle = (−g, −f)
∴ Radius of the circle = \tt \sqrt{g^{2}+f^{2}-c}
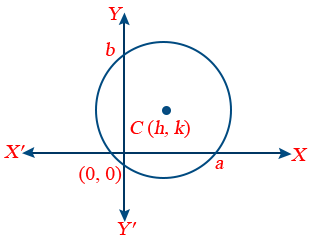
2. Equation of circle having centre (h, k) and radius a is (x − h)2 + (y − k)2 = a2.
If centre is (0, 0), then equation of circle is x2 + y2 = a2.
3. When the circle passes through the origin, then equation of the circle is x2 + y2 − 2hx − 2ky = 0.
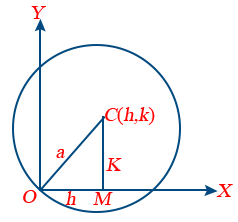
4. When the circle touches the X-axis, the equation is x2 + y2 − 2hx − 2ay + h2 = 0.
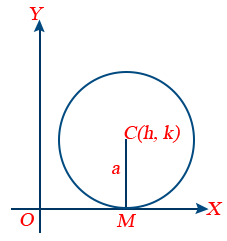
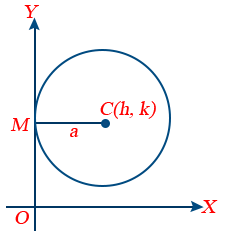
5. Equation of the circle, touching the Y-axis is x2 + y2 − 2ax − 2ky + k2 = 0.
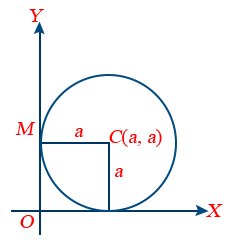
6. Equation of the circle, touching both axes is x2 + y2 − 2ax − 2ay + a2 = 0.
7. Equation of the circle passing through the origin and centre lying on the X-axis is x2 + y2 − 2ax = 0.
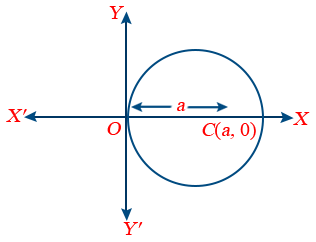
8. Equation of the circle passing through the origin and centre lying on the Y-axis is x2 + y2 − 2ay = 0.
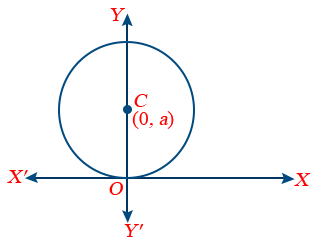
9. Equation of the circle through the origin and cutting intercepts a and b on the coordinate axes is x2 + y2 − by = 0.
10. Equation of the circle, when the coordinates of end points of a diameter are (x1 , y1) and (x2 , y2) is
(x − x1) (x − x2) + (y − y1) (y − y2) = 0.
11. Equation of the circle passes through three given points (x1 , y1) , (x2 , y2) and (x3 , y3) is \tt \begin{vmatrix}x^{2}+ y^{2} & x & y & 1 \\ x_1^2 + y_1^2 & x_1 & y_1 & 1 & \\ x_2^2 + y_2^2 & x_2 & y_2 & 1 \\ x_3^2 + y_3^2 & x_3 & y_3 & 1 \end{vmatrix}=0.
12. Parametric equation of a circle (x − h)2 + (y − k)2 = a2 is x = h + a cos θ , y = k + a sin θ , 0 ≤ θ ≤ 2π
For circle x2 + y2 = a2 , parametric equation is x = a cos θ , y = a sin θ

13. The equation of the tangent at the point P(x1 , y1) to a circle x2 + y2 + 2gx + 2fy + c = 0 is xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
14. The equation of the tangent at the point P(x1 , y1) to a circle x2 + y2 = r2 is xx1 + yy1 = r2.
15. The equation of the tangent of slope m to the circle x2 + y2 + 2gx + 2fy + c = 0 are \tt y+f=m\left(x+g\right)\pm\sqrt{\left(g^{2}+f^{2}-c\right)\left(1+m^{2}\right)}
Parametric Form
1. The equation of the tangent to the circle (x − a)2 + (y − b)2 = r2 at the point (a + r cos θ, b + r sin θ) is (x − a) cos θ + (y − b) sin θ = r.
2. The equation of normal at the point (x1, y1) to the circle x2 + y2 + 2gx + 2fy + c = 0 is
\tt y-y_{1}=\frac{y_{1}+f}{x_{1}+g}\left(x-x_{1}\right)
(y1 + f) x − (x1 + g) y + (gy1 − fx1) = 0
3. The equation of normal at the point (x1 , y1) to the circle x2 + y2 = r2 is \tt \frac{x}{x_{1}}=\frac{y}{y_{1}}.
4. The equation of normal to the circle x 2 + y2 = r2 at the point (r cos θ, r sin θ) is
\tt \frac{x}{r \cos \theta}=\frac{y}{r \sin \theta}
y = x tan θ.

