States of Matter: Gases and Liquids
Real Gases, Compressibility Factor, Vander Waal Equation
Ideal gas:
- The gas that obeys all gas laws at 'T' and 'P' is called real gas.
- Real gas obeys Ideal behaviour at low pressure and high temperature.
Compressibility factor (Z):
It is denoted by 'Z'
\tt Z=\frac{V_{obs}}{V_{ideal}}=\frac{V_{0}P}{nRT} (PV = nRT)
\tt Z=\frac{V_{0}P}{RT} (n = 1)
Z ∝ PV0
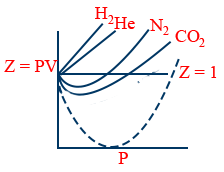
At low pressure:
\tt From\ \left(P+\frac{a}{V^2}\right)\left(V-b\right)=RT for 1 mole of gas
\tt \ \left(P+\frac{a}{V^2}\right)(V)=RT
\tt PV = RT-\frac{a}{V}
\tt \frac{PV}{RT}=1-\frac{a}{RTV}
\tt Z=1-\frac{a}{RTV} At low pressure Z=−ve, shows −ve deviation.
At High pressure:
P(V−b) = RT ⇒ PV − Pb = RT
PV = Pb + RT
\tt \frac{PV}{RT}=\frac{Pb}{RT}+1
\tt Z=1+\frac{Pb}{RT}
Abnormal behaviour of H2 and He
\tt \frac{PV}{RT}=1+\frac{Pb}{RT}\Rightarrow Z=\frac{1+Pb}{RT}
View the Topic in this Video from 2:16 to 36:30
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. The Vander Waal's equation for n moles of the gas is, \tt \left(P + \frac{n^{2}a}{V^{2}}\right) \left[V - nb\right] = nRT
\tt \left(P + \frac{n^{2}a}{V^{2}}\right) = Pressure correction for molecular attraction, \tt \left[V - nb\right] = Volume correction for finite size of molecules
2. Molar heat capacity of a substance is the quantity of heat required to raise the temperature of 1 mole of the substance by 1° C.
∴ Molar heat capacity = Specific heat capacity × Molecular weight, i.e., Cv = cv × M and Cp = cp × M

