Classification of Elements and Periodicity in Properties
Atomic Radii, Ionic Radii, Ionization Energy, Electron affinity, Electronegativity
Periodicity and Properties :
Repetition of similar properties at regular intervals
→ IA, II A, 0 → 2, 8, 8, 18, 18, 32
→ III A - VI A → 8, 18, 18, 32
- Atomic Radius
- Ionization potential
- Electron Affinity
- Electron Negativity
- Metallic and Non-metallic
- Valency
- Electropositivity
- Nature of oxides.
Atomic Radius :
Distance between nucleus and outermost electron. expressed in Å, nm, and pm etc ....Experimental determination of atomic radius is not possible. Atoms have no sharp boundary.
 ⇒ Radius of H - atom \frac{D_{H - H}}{2}=\frac{0.74}{2} = 0.37Å
⇒ Radius of H - atom \frac{D_{H - H}}{2}=\frac{0.74}{2} = 0.37Å
Crystal Radius / Metallic Radius :
Half of the inter nuclear distance between two nucleus

r_{Na} = \frac{d_{{Na} - {Na}}}{2}
Vander Waal's Radius :
→ minimum force between particles
→ size increases vander waal's force of attraction(VWFOA) increases.
Cl2 ----- Cl2 , VWFOA is in between two chlorine molecules
VR > MR > CR
VR = vander waal's
MR = metallic radius
CR = crystal radius
Factors influencing atomic radius :
effective nuclear charge (Z*)
\tt Z^{*} = \left(\frac{No.of \ protons}{No.of \ electrons}\right)
Na^{+} = \frac{11}{10},\ Mg^{+2} = \frac{12}{10}, \ Al^{+3} = \frac{13}{10}
Factors influencing ionization energy :
→ Atomic radius :
IP \ (or) \ IE \propto \frac{1}{AR}
Nuclear charge : Increases left to right
Screening / shielding effect :
s > p > d > f
IP \propto \frac{1}{Screening}
Half - filled and completely filled sub-shells :
C N O
2s22p2 2s22p3 2s22p5
As it has half filled ⇒ more stable.
Zn 4s23d10 completely filled-more stable.
Effective nuclear charge (Z*) and screening constant :
Z* = Z − σ (Z = atomic number)
Screening Constant(σ) :
following slates rule
electrons from nth shell → 0.35
electrons from (n − 1) shell → 0.85
electrons (n − 2) and inner shells → 1.0
C : 1s2 2s2 2p2
1s2 2s2 2p1 + \upharpoonleft
σ = 3(0.35) + 2(0.85) = 2.75
Z* = 6 − 2.75 = 3.25
Lanthanoid Contraction :
→ differentiating e− enters into deep seated 4f - orbitals
shielding : s > p > d > f
→ due to poor shielding capacity of 4f - orbitals
→ size decreases gradually.
Consequences of Lanthanoid Contraction :
→ atomic size of 4d, 5d series elements are almost same.
eg : Zr - Hf, Nb - Ta ----
→ IP values of 5d - series elements are more than those of 4d - series elements.
Basic nature and covalent nature of hydroxides decreases from Ce(OH)3 → Lu(OH)3
Ionization Potential :
Amount of energy required to remove the most loosely held electron from an isolated neutral gaseous atom.
Xg + IP (or) IE1 → X_g^{+} + e−
ΔH = +IE
1 e.V = 3.35 × 10-20 cal/atom
= 1.6 × 10-19 J/atom
= 96.45 kJ/mol
= 23.06 kcal/mol.
Electron Gain Enthalpy(ΔegH) :
X_{(g)} + e^{-}\rightarrow X_g^{{-}}, \triangle H = -EA_{1}
Note : except for Be, Mg, N, He, Ne, Ar, Kr, Xe
EA1 is always positive
\triangle_{eg}H = -E_{A} - \frac{5}{2}RT
X_{(g)}^- + e^{-} \rightarrow X_{(g)}^{2-} ; \triangle H_{2} = +EA_{2} is endothermic
Electronegativity : Tendency of the bonded atom to attract the bonding e−
Pauling Scale of EN :
X_{A} - X_{B} = 0.208\sqrt{\triangle}
Δ is in kcal/mole
X_{A} - X_{B} = 0.1017\sqrt{\triangle}
Δ is in kJ/mole
\triangle = \left(E_{A - B}\right)_{exp} - \frac{1}{2}\left(E_{A - A} - E_{B - B}\right)_{theoretical}
Mulliken's Scale of EN :
EN = \frac{IP + EA}{2}
case (1) EN = \frac{I_{P} + E_{A}}{2 \times 2.8}
= \frac{IP + EA}{5.6} (in \ e.V)
= \frac{IP + EA}{130}(kcal / mol)
= \frac{IP + EA}{544}(kJ / mol)
Hybridization :
As the s - character of hybrid orbital increases EN ↑
| %S | EN | |
| sp3 | 25 % | 2.55 |
| sp2 | 33.33 % | 2.75 |
| sp | 50 % | 3.25 |
sp > sp2 > sp3
Electronegativity Applications :
% of ionic character = 16 (XA − XB) + 3.5(XA − XB)2
electronegativity difference = 1.7 ⇒ 50% covalent character
⇒ 50% ionic character
= 0 ⇒ 100% covalent character
< 1.7 ⇒ more than 50% covalent
> 1.7 ⇒ more than 50% ionic
Part1: View the Topic in this Video from 0:12 to 9:52
Part2: View the Topic in this Video from 0:12 to 10:34
Part3: View the Topic in this Video from 0:12 to 8:55
Part4: View the Topic in this Video from 0:12 to 11:11
Part5: View the Topic in this Video from 0:12 to 9:08
Part6: View the Topic in this Video from 0:11 to 10:56
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Atomic radius,\tt r_{A}=\frac{r_{A}+r_{A}}{2}=\frac{d_{A-A}}{2}
[DistanceA-A = radius of A + radius of A]
2. For heterodiatomic molecule AB, dA-B = rA + rB + 0.09 (XA-XB)
where, XA and XB are electronegativities of A and B.
3. Mulliken scale
Electronegativity (x) =\tt \frac{IE+\Delta He_{g}}{2}
4. Pauling scale: The difference in electronegativity of two atoms A and B is given by the relationship \tt x_{B}-x_{A}= 0.208\sqrt{\Delta}
where, \tt \Delta = E_{A-B}-\sqrt{E_{A-A}\times E_{B-B}}
(Δ is known as resonance energy.)
EA-B, EA-A and EB-B represent bond dissociation energies of the bonds A - B, A - A and B - B respectively.
5. Allred and Rochow's scale
Electronegativity =\tt 0.744+\frac{0.359\ Z_{eff}}{r^{2}}
where, Zeff is the effective nuclear charge = Z − σ
where, σ is screening constant. It's value can be determined by Slater's rule.
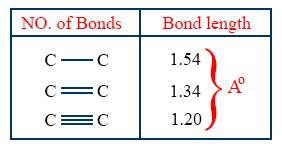
6. Covalent radius
rcovalent or \tt r_{c}= \frac{1}{2} [bond length]
7. The screening effect and effective nuclear charge are very closely related, i.e,
Z' = Z − σ
where, Z' = effective nuclear charge
Z = atomic number
σ = screening constant

