Electromagnetic Induction
The Experiments of Faraday and Henry, Magnetic Flux
- The magnetic flux through a surface (area \tt \overrightarrow{A}) placed in a uniform magnetic field \tt \overrightarrow{B} is defined as \tt \phi \overrightarrow{B} \cdot \overrightarrow{A}= BA \cos \theta
Where θ is the angle between \tt \overrightarrow{B} and \tt \overrightarrow{A}
- If there is a change of magnetic flux in a circuit, there will be an induced emf and this will last until the change persists, is FARADAY’S LAW.
- The magnitude of induced emf is equal to the time rate of change of magnetic flux \tt e = \frac{d \phi}{dt}
- The polarity of the induced emf tends to produce a current which opposes the change that produces it. This is known as LENZ’S LAW




- φ = BAN cos θ, the change in flux can be caused by changing B (or) A or N
- Only when ‘B’ is changed, the average induced emf is, \tt e = - AN \cos \theta \frac{(B_{2} - B_{1})}{(t_{2} - t_{1})}
- Only when ‘A’ is changed, the average induced emf is given by, \tt e = - BN \cos \theta \frac{(A_{2} - A_{1})}{(t_{2} - t_{1})}
- Only when ‘θ’ is change, the average induced emf is, \tt e = - BAN \frac{(\cos \theta_{2} - \cos \theta_{1})}{(t_{2} - t_{1})}
- When the coil is rotated with constant angular velocity ‘ω’, then \tt e = - BAN \frac{d(\cos \omega t)}{dt} = BAN \omega \ sin \omega t
- The change in flux by changing the number of turns is practically difficult.
- The current induced in a coil is given by \tt i = \frac{e}{R} = \frac{-1}{R} \frac{\Delta \phi}{\Delta t}
- \tt q = - \frac{\Delta \phi}{R} \left(i = \frac{q}{\Delta t}\right)
- If a rod of length ‘l’ is moved with a velocity ‘v’ perpendicular to its length in a uniform magnetic field B which is perpendicular to both its length as well as its velocity, then e = Blv
- If the rod is moved making an angle ‘θ’ with its length, then e = Blv sin θ
- FLEMINGS RIGHT HAND RULE : Stretch the thumb, fore finger and middle finger such that they all are mutually perpendicular to each other.
- If Thumb represents – direction of velocity
Forefingers represents – direction of field
Middle finger represents – direction of induced current
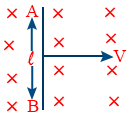
- If ends of the rod A and B are connected by an external resistance R, then the current in the rod is given as, \tt i = \frac{Blv}{R}
- The force acting on the rod due to current carrying conductor, \tt F = Bil \Rightarrow F = \frac{B^{2} l^{2} v}{R} \left(i = \frac{Blv}{R}\right)
- To move the rod with constant velocity, the power applied by external agent is \tt P = F V = \frac{B^{2} l^{2} v^{2}}{R}
- A rod of length l is rotated about O perpendicular to its length in an uniform magnetic field B, then emf, \tt e = \frac{1}{2} B l^{2} \omega
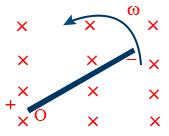
- A rod is rotated about an axis passing through its centre, O and perpendicular to its length then emf across the ends is zero.
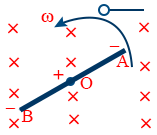
- emf across \tt OB = \frac{-1}{8} B l^{2} \omega
- emf across \tt OA = + \frac{1}{8} B l^{2} \omega
- The flow patterns of induced currents resemble the swirling eddies in water and these currents are called EDDY CURRENT (OR) FOUCAULT CURRENTS
- The eddy currents are reduced by using laminations of metal to make a metal core. Insulating material like lacquer is used to separate laminations.
- When the current flowing in one coil changes, magnetic flux linked with the second coil placed near to it also changes. The emf induced in secondary coil is called mutually induced emf. This phenomenon is known as MUTUAL INDUCTION
View the Topic in this video From 1:03 To 56:32
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. The magnetic Net flux through the surface \phi = \oint \overrightarrow{B}. d \overrightarrow{A} = BA \cos \theta

