Electric Charges and Fields
Electric Flux, Electric Dipole and Gaus's Law
- Electric flux is defined as the dot product of Electric field intensity and Area \tt \phi = \overline{E} \cdot \overline{A}
- According to Gauss law the total flux linked with Gaussion surface is \tt \frac{1}{\varepsilon_{0}} times the net charge. \tt \phi = \oint \overline{E} \cdot \overline{d} A = \frac{q}{\varepsilon_{0}}
- If charge is kept at the centre of a cube then flux through cube = \tt \frac{Q}{\varepsilon_{0}} flux through face = \tt \frac{Q}{6 \varepsilon_{0}}
- If charge is kept at the centre of face then flux through cube = \tt \frac{Q}{2 \varepsilon_{0}}
- If charge is kept at the corner of a cube then flux from cube = \tt \frac{Q}{8 \varepsilon_{0}}. \phi_{face} = \frac{Q}{24 \varepsilon_{0}}
- Electric field at a distance ‘r’ from the axis of a long straight charged wire \tt E = \frac{\lambda}{2 \pi \varepsilon_{0} r}
- Electric potential at a distance r from the axis of a long straight charged wire \tt v = \frac{- \lambda}{2 \pi \varepsilon_{0}} \log_{e}^{r} + K
- Electric field due to a thin infinite sheet (Non conducting) \tt E = \frac{\sigma}{2 \varepsilon_{0}}
- Electrostatic potential due to a thin infinite sheet \tt V= - \frac{\sigma}{2 \varepsilon_{0}} r + K
- Electric field due to a thick infinite sheet (Non conducting) \tt E = \frac{\sigma}{\varepsilon_{0}}. and V = - \frac{\sigma}{\varepsilon_{0}} r + K
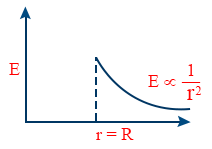
- Electric field due to a charged hollow sphere at a point out side the sphere \tt E = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q}{r}^{2} = \frac{\sigma R^{2}}{\varepsilon_{0} r^{2}} \left(r \gt R\right)
- Electric field due to a charged hollow sphere at a point on the sphere \tt E = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q}{r}^{2} = \frac{\sigma }{\varepsilon_{0}}
- Electric field due to a charged hollow sphere inside E = o.
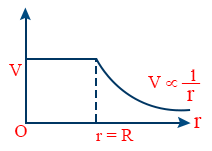
- Electric potential due to a charged hollow sphere at a point outside the sphere \tt V = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q}{r} \left(r \gt R \right)
- Electric potential due to a charged hollow sphere at a point on the surface \tt V = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q}{R} \left(r = R \right)
- V inside sphere = \tt \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q}{R}
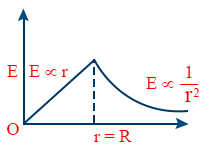
- Electric field ‘E’ due to a uniformly charged Non conducting sphere E out \tt E_{out} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q}{r^{2}} = \frac{\rho R^{3}}{3 \varepsilon_{0} r^{2}}
- E at the surface = \tt = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q}{R^{2}} = \frac{\rho R}{3 \varepsilon_{0}}
- E inside = \tt = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Qr}{R^{3}} = \frac{\rho R}{3 \varepsilon_{0}}
- E, r graph for a hollow sphere
- E, r graph for a conducing sphere
- V, r graph for a hollow sphere
- Electric potential due to spherical charge distribution \tt V_{out} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{r} \ \ V_{surface} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{R}
- Electric potential due to spherical charge distribution \tt V_{inside} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{2R} \left[3 - \frac{r^{2}}{R^{2}}\right]
V, r graph for spherical charge distribution
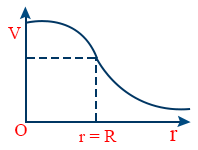
- Electric field at the axis of a circular uniformly charged ring \tt E = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Qr}{\left(R^{2} + r^{2}\right)^{3/2}}
- Electric field at the centre of a uniformly charged ring E = O.
- Electric potential due to uniformly charged disc at a distance ‘r’ \tt V = \frac{\sigma}{2 \varepsilon_{0}} \left[\sqrt{R^{2} + r^{2}} -r \right]
- At centre r = o \tt \therefore V = \frac{\sigma R}{2 \varepsilon_{0}}
- Electrostatic potential energy of system of two charges q1 and q2 separated by ‘d’. \tt U = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{1} q_{2}}{d}
- Electrostatic potential Energy of system of three charges q1, q2 and q3 \tt U = \frac{1}{4 \pi \varepsilon_{0}} \left[\frac{q_{1}q_{2}}{d_{1}} + \frac{q_{2}q_{3}}{d} +\frac{q_{3}q_{1}}{d}\right]
- Two charges separated by a distance ‘d’ are left free. The gain in \tt KE = \frac{1}{8 \pi \varepsilon_{0}} \cdot \frac{q_{1} q_{2}}{d}
- Equation for two charges left free separated by ‘d’ \tt \frac{1}{2} mv^{2} + \frac{1}{2} mv^{2} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{1} q_{2}}{d}
- The amount of Energy gained by an electron when accelerated through a potential difference of one volt is Electron volt
- 1 ev = 1.6 × 10−19 Joules.
- Work done in rotating an electric dipole W = PE (cos θ1 − cos θ2)
- When θ1 = 0° θ2 = θ u = w = −PE cos θ
- When θ1 = 0 θ2 = 90° u = w = PE
- For a metal conductor kept in Electric field the field inside the conductor is zero.
- The resultant electric field when a Dielectric is placed in an External field E = EApplied field – Einduced field
- Induced field Ei = EApplied \tt \left(1-\frac{1}{K}\right) (K = Dielectric const)
- Induced charge on the surface \tt q_{i} = - q_{0} \left(1-\frac{1}{K}\right)
- Dielectric polarisation is defined as the dipole moment per unit volume of the dielectric.
- The relation between Electric displacement and polarisation. \tt \overline{D} = \varepsilon_{0} \overline{E} + \overline{P} (\tt \overline{P} = Dielectric polarisation, D = Electric displacement)
- The electric susceptibility (Χe) and Dielectric polarisation are related as P = Χe E
- The electric susceptibility Χe = (K – 1) ε0
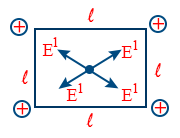
- Electric field intensity at the centre is zero (E = 0)
- Two equal and opposite charges separated by a fixed distance (2a) is called and electric dipole
- The electric dipole moment \tt \overline{P} = q \left(2\overline{a}\right)
- The direction of Electric dipole moment is from Negative charge to positive charge.
- Torque acting on Electric dipole Τ = PE sin θ.
- Electric field on the axial line of an electric dipole \tt E_{a} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{2Pr}{\left(r^{2} - a^{2}\right)^{2}}
- Electric field on the Equatorial line of an electric dipole \tt E_{eq} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{P}{\left(r^{2} + a^{2}\right)^{3/2}}
- Electric field on the axial line of a short dipole \tt E_{a} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{2P}{r^{3}}
- Electric field on the Equatorial line of a short dipole \tt E_{eq} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{P}{r^{3}}
- \tt \frac{E_{axial}}{E_{equitorial}} = 2
- Electric field due to short dipole at any point \tt E_{eq} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{P}{r^{3}} \sqrt{1 + 3 \cos^{2} \theta}
- n oil drops of radius ‘r’ and charge ‘q’ are merged to form a big drop of radius R charge Q. Then Radius of Big drop R = n1/3 r
- Charge on Big drop Q = nq
- Energy of Big drop U = n2/3 . Usmall
- Electric field due to Big drop E = n1/3 . Esmall
- Surface charge density of Big drop σBig = n1/3 . σsmall
- Potential of Big drop VBig = n2/3 Vsmall
- Electric force between two dipoles placed coaxially \tt F = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{6 P_{1}P_{2}}{r4}
- Electric force between two dipoles placed perpendicular to each other \tt F = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{3 P_{1}P_{2}}{r4}
- Angular frequency (ω) of electric dipole in uniform electric field \tt \omega = \sqrt{\frac{PE}{I}}
- (I = moment of inertia)
- The electric dipole moment of the system is \tt \sqrt{3ql}

Electric Dipole: View the Topic in this video From 41:56 To 54:10
Gauss Law and Electric Flux
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Flux of electric field \tt \overrightarrow{E} through any area \tt \overrightarrow{A} is defined as
\tt \phi=E.A\cos \theta\ or\ \phi=\overrightarrow{E}.\overrightarrow{A}
2. In case of variable electric field or curved area. \tt \phi = \int \overrightarrow{E}.\overrightarrow{dA}
3. Electric Field Intensity on Axial Line
At the distance r from the centre of the electric dipole, \tt E=\frac{1}{4\pi \varepsilon_{0}}-\frac{2pr}{\left(r^2-a^2\right)^2}
4. Electric Field Intensity on Equatorial Line: At the point at a distance r from the centre of electric dipole, \tt E=\frac{1}{4\pi \varepsilon_{0}}\frac{p}{\left(r^2-a^2\right)^{3/2}}
5. The flux through an area element ΔS is
\tt \Delta \phi=E\cdot\Delta S=\frac{q}{4\pi\varepsilon_0r^2}\hat{r}\cdot\Delta S

