Electric Charges and Fields
Electric Field and Electric Field Lines
- Electric field intensity is defined as the force experienced by a unit positive charge placed at a point \tt E = \frac{F}{q}
- If intensity is same at every point both in magnitude and direction it is said to be uniform field.
- If intensity is different at different points then it is Non uniform field.
- Force acting on a charged particle at rest in uniform field is F = Eq.
- Acceleration of a charged particle starting from rest in a uniform field is \tt a = \frac{Eq}{m}
- Final velocity \tt v = \left(\frac{Eq}{m}\right) t & momentum p = (Eq)t
- Displacement \tt S = \frac{1}{2} \left(\frac{Eq}{m}\right)t^{2}
- Kinetic energy oKE = \tt \frac{1}{2} \left(\frac{Eq}{m}\right)^{2} t^{2}
- Null point is the point where the resultant electric field intensity becomes zero.
- Position of null point when charges q1 & q2 are separated by a distance d is \tt x = \frac{d}{\sqrt{\frac{q_{2}}{q_{1}}} \pm 1} where {+ like charges and − unlike charges}
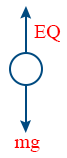
- Equilibrium condition of charge is EQ = mg
- When charge is suspended from a string
T sin θ = Eq
T cos θ = mg
\tt \tan \theta = \frac{Eq}{mg}
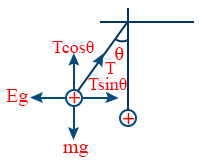
- Tension in the string \tt T = \sqrt{(Eq)^{2} + (mg)^{2}}
- When two identical charged spheres of same mass are suspended by strings of same length
- \tt \frac{F}{l \sin \theta} = \frac{w}{l \cos \theta} = \frac{T}{l} \left\{F = \frac{1}{4 \pi \varepsilon_{0}} \frac{q^{2}}{n^{2}}\right\}
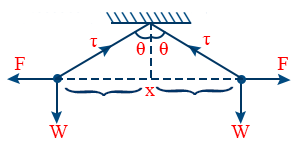
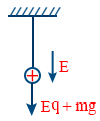
- Time period of oscillation of a charged body in electric field \tt T = 2 \pi \sqrt{\frac{l}{\left(g + \frac{Eq}{m}\right)}}
- A line of force is the path along which a unit positive charge accelerates in Electric field.
- Lines of force diverge from positive charge and converge to negative charge.
- The tangent at any point to line of force gives the direction of the field at that point.
- Lines of force never intersect.
View the Topic in this video From 3:53 To 41:44
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Electric field intensity (\overrightarrow{E}): The electric field intensity at any point is defined as the force experienced by a unit positive charge placed at that point.
\overrightarrow{E} = \frac{\overrightarrow{F}}{q_{0}} = \frac{kQ}{r^{2}}
2. Charge may not affect the source charge Q and its electric field is not changed, for electric field intensity
\overrightarrow{E} = \lim_{q_{0} \rightarrow 0} \frac{\overrightarrow{F}}{q_{0}}
3. Electric field intensity and electric potential due to a point charge q, at a distance t1 + t2 where t1 is thickness of medium of dielectric constant K1 and t2 is thickness of medium of dielectric constant K2 are:
E = \frac{1}{4 \pi \varepsilon_{0}}\frac{Q}{\left(t_{1}\sqrt{K_{1}} + t_{2}\sqrt{K_{2}}\right)^{2}}; V = \frac{1}{4 \pi \varepsilon_{0}}\frac{Q}{\left(t_{1}\sqrt{K_{1}} + t_{2}\sqrt{K_{2}}\right)}

