Dual Nature of Matter and Radiation
Wave Theory of Light, Einstein’s Photoelectric Equation and Particle Nature of Light
- ELNSTEIN’S PHOTO ELECTRIC EQUATION : \tt h\nu=h\nu_{0}\ +\ \frac{1}{2}\ mV_{max}^2
- \tt \frac{1}{2}\ mV_{max}^{2}\ =\ h\left(\nu-\nu_0\right)=hc\left(\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right)
- \tt V_{max}=\sqrt{\frac{2h\left(\nu-\nu_{0}\right)}{m}}=\sqrt{\frac{2\ hc}{m}\frac{\left[\lambda_{0}-\lambda\right]}{\lambda\ \lambda_{0}}}
- \tt \frac{\left[K\ E_{max}\right]_1}{\left[K\ E_{max}\right]_2}=\frac{h\nu_{1}-W}{h\nu_{2}-W}=\frac{\nu_{1}-\nu_{0}}{\nu_{2}-\nu_{0}}
- \tt \frac{\left[K\ E_{max}\right]_1}{\left[K\ E_{max}\right]_2}=\frac{hc\left(\frac{1}{\lambda_{1}}-\frac{1}{\lambda_{0}}\right)}{{hc\left(\frac{1}{\lambda_{2}}-\frac{1}{\lambda_{0}}\right)}}=\frac{\left(\frac{1}{\lambda_{1}}-\frac{1}{\lambda_{0}}\right)}{{\left(\frac{1}{\lambda_{2}}-\frac{1}{\lambda_{0}}\right)}}
- Energy of photon in eV = \tt E=\frac{12400}{\lambda\left(in\ Angstrom\right)} in eV
- Work function = \tt W= \frac{12400}{\lambda_{0}} in e.V
- The graph between maximum kinetic Energy and maximum velocity increases linearly with the frequency of the incident radiation.
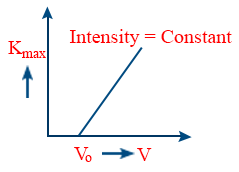
-
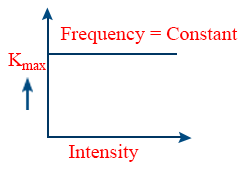
-

- The photoelectric effect is an instantaneous phenomenon. The time lag between incidence of radiation and emissions of photo electron is very small.
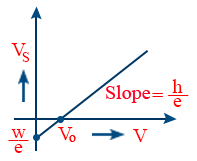
- The graph between stopping potential, Vs and incident frequency (ν) is a straight line with slope \tt \frac{h}{e}
- The graph between K.Emax and incident frequency, ν is a straight line with slope h
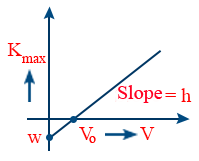
- In photoelectric effect all the emitted photoelectrons do not have same kinetic energy. The K.E ranges from 0 to K.Emax (or) 0 to h (ν – ν0)
- Intensity of the radiation obeys inverse square law \tt I\propto\frac{1}{d^{2}}\ and\ i\propto I\Rightarrow\ i\propto\ \frac{1}{d^{2}}
- Photo electric Cells convert light energy to electrical energy.
- Vacuum type of photo emissive cells has instantaneous response.
- In gas filled photo emissive cells, photo current will not be proportional to intensity of the incident radiation.
- In the perspective of De.Broglie, matter behaves both as particles and waves.
- de-BROGLIE wavelength associated with the matter wave of that particle is \tt \lambda=\frac{h}{mv}=\frac{h}{p}=\frac{h}{\sqrt{2mE}}
- de-BROGLIE wave equation: \tt \lambda\propto\frac{1}{\nu} & if ν = 0, λ = ∞
- \tt \lambda\propto\frac{1}{m} {λ = de-Broglie wavelength m = mass}
- \tt \lambda\propto\frac{1}{p} {λ = de-Broglie wavelength P = momentum}
- \tt \lambda\propto\frac{h}{\sqrt{2\ mqv}}{ν = potential difference h = plancks constant q = charge}
- For an electron \tt \lambda\approx\frac{12.27}{\sqrt{v}}\ A^{o}
- For a proton, \tt \lambda=\frac{0.286}{\sqrt{v}}\ A^{o}
- For deuteron, \tt \lambda=\frac{0.202}{\sqrt{E}}\ A^{o}
- For α particle, \tt \lambda=\frac{0.101}{\sqrt{v}}\ A^{o}
- For neutron, \tt \lambda=\frac{0.286}{\sqrt{E}}\ A^{o}
- If the de Broglie waves are associated with electron, then these should be diffracted like x-rays. we can determine the wave length of these waves using the Bragg’s formula, 2d sin θ = n λ
- \tt \theta=\left[\frac{180-\phi}{2}\right] = Bragg’s angle
- de Broglie wave length can also be verified using the formula \tt \lambda=\frac{12.27}{\sqrt{v}}=\frac{12.27}{\sqrt{54}}=1.67\ A^{o}
- X-rays are produced by the deceleration of high energy electrons bombarding a hard metal target.
- The target used to produce x-rays should have a) high atomic weight b) high melting point c) high thermal conductivity.
- X-rays are electromagnetic waves of very short wavelength i.e order of wave length 0.1 Å – 100Å, order of frequency 1016 Hz – 1019 Hz, order of energy 124eV – 124 KeV
- Intensity of x-rays depends on the number of electron striking the target
- High frequency x-rays are called HARD X-RAYS.
- Low frequency X-rays are called SOFT X-RAYS.
- CONTINUOUS X-RAY SPECTROM is produced when high speed electron are suddenly stopped by a metal target.
- Continuous X-ray spectrum contains all wave lengths above a minimum wavelength λm
- \tt \lambda_{min}=\frac{hc}{eV}=\frac{12400}{v}\ A^{o}
- \tt \nu_{max}=\frac{eV}{h}, maximum frequency of emitted X-ray photon.
- Efficiency of X-ray tube, \tt \eta=\frac{output\ power}{input\ power}\times100
- CHARACTERISTIC X-RAY SPECTRUM is produced due to transition of electrons from higher energy level to lower energy level in target atoms.
- Wavelengths of the X-rays of characteristic X-ray spectrum depend only on atomic number of the target element and independent of target potential.
- In characteristic X-rays, K-series of lines are obtained when transition takes place from higher levels to K-shell.
- EKα < EKβ < EKγ, EKα > ELα
- IKα > IKβ > IKγ
- \tt \nu_{k\beta} = \nu_{k\alpha} + \nu_{L\alpha} \Rightarrow \frac{1}{\lambda_{k\beta}} =\frac{1}{\lambda_{k\alpha}} + \frac{1}{\lambda_{L\alpha}}
- \tt E_{k} - E_{L} = h\nu_{k\alpha} = \frac{hc}{\lambda_{k\alpha}}
View the Topic in this video From 00:19 To 28:33
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. The balance of the photon energy is used up in giving the electron a kinetic energy of \frac{1}{2}mv^{2}
hv = \phi_{0} + \frac{1}{2}mv^{2}
2. Kinetic energy of photoelectrons is ΔKE = hv − hv0 = h(v − v0)
= hc \left[\frac{1}{\lambda} - \frac{1}{\lambda_{0}}\right] = 12400 \left[\frac{1}{\lambda (A^0)} - \frac{1}{\lambda_{0}(A^0)}\right]eV

