Dual Nature of Matter and Radiation
Wave Nature of Matter, Davisson and Germer Experiment
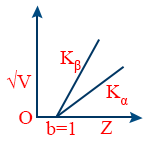
- The square root of frequency, (ν) of the spectral line of the characteristic X-ray spectrum is directly proportional to the atomic number, Z of the target element.
- \tt \sqrt{V} \propto Z \ or \ \sqrt{V} = a(z - b)
-
For K -series (Characteristic x -ray spectrum)
\tt \sqrt{\frac{\nu_{1}}{\nu_{2}}} = \left(\frac{Z_{1} - 1}{Z_{2} - 1}\right) \Rightarrow \sqrt{\frac{\lambda_{1}}{\lambda_{2}}} = \left(\frac{Z_{1} - 1}{Z_{2} - 1}\right) - The intercept on Z-axis gives the screening constant ‘b’ and it is constant for all spectral lines in given series but varies with the series.
b = 1 for K series (Kα | Kβ | Kγ)
b = 7.4 for L series.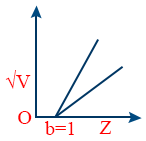
-
The wave lengths of characteristics x -rays is given by \tt \frac{1}{\lambda} = R\left(z - b\right)^{2}\left[\frac{1}{n_1^2} - \frac{1}{n_2^2}\right]
- \tt \frac{\lambda_{k\alpha}}{\lambda_{k\beta}} = \frac{32}{27} , Ratio of kα and kβ lines
- DAVISSON AND GERMER'S ELECTRON DIFFRACTION EXPERIMENT gives the evidence of matter wave existence.
- A beam of electron emitted by electron gun is made to fall on mickel crystal and along cubical axis at a particular angle
- Ni crystal behaves like a 3 dimensional diffraction grating and it diffracts the electron beam obtained from electron gun.
- The diffracted beam of electron received by the detector which can be positioned at any angle by rotating about the point of incidence.
- The energy of the incident beam of electron can also be varied by changing the applied voltage to the electron gun.
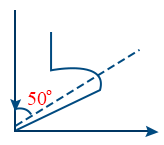
- Intensity of scattered beam of electrons was different at different angles of scattering.
- Intensity bump is maximum for 54 V potential and 50° scattering angle.
View the Topic in this video From 00:19 To 09:24
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. The wavelength associated with a moving particle is known as de Broglie wavelength and it is given by
\lambda = \frac{h}{p} = \frac{h}{mv}
2. KE = \frac{P^{2}}{2m} \Rightarrow \lambda = \frac{h}{\sqrt{2 m \ KE}}
3. De Broglie wavelength associated with charged particles
For electrons (mc = 9.1 × 10−31 kg):
\lambda = \frac{h}{\sqrt{2mqV}}
4. De Broglie wavelength associated with uncharged particles
For neutrons (mn = 1.67 × 10−27 kg):
\lambda = \frac{h}{\sqrt{2mE}} = \frac{6.62 \times 10^{-34}}{\sqrt{2 \times 1.67 \times 10^{-27}E}}
5. de Broglie wavelength & wave nature
\lambda = \frac{h}{mv} = \frac{6.63 \times 10^{-34}}{(0.046)(30)} = 4.8 \times 10^{-34} m
6.The de Broglie wavelength λ associated with electrons using, for V = 54 V is given by davission & German Experiment
\tt \lambda = h/p = \frac{1.227}{\sqrt{V}}nm

