Current Electricity
Combination of Resistors-Series and Parallel
- Rseries = R1 + R2 + R3 + …….
- When 'n' identical resistances are connected Rseries = nR.
- When resistances are connected in series V1 : V2 : V3 = R1 : R2 : R3.
- When resistances are connected in series V = V1 + V2 + V3.
- In parallel combination potential is constant across the ends of resistances.
- In parallel combination i1 : i2 : i3 = \tt \frac{1}{R_{1}} : \frac{1}{R_{2}} : \frac{1}{R_{3}}
- In parallel combination i = i1 + i2 + i3.
- In parallel combination \tt \frac{1}{R_{Eff}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}
- When ‘n’ equal resistances are connected in parallel \tt R_{Eff} = \frac{R}{n}
- If ‘n’ wires each of resistance "R" are connected to form a closed polygon \tt R_{Eff} = \frac{(n-1)}{n} R.
- A resistance wire ‘R’ is in the form of a circle. The resistance across diametric ends. \tt R_{Eff} = \frac{R}{4}
-
A wire bent in the form of a circle \tt R_{AB} = \frac{R \theta (2 \pi - \theta)}{4 \pi r^{2}}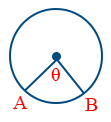
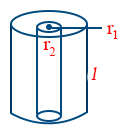
- Resistance of a hollow cylinder \tt R = \frac{\rho \ l}{\pi \left(r_{1}^{2} - v_{2}^{2}\right)}
- 12 wires each of resistance "r" are connected in the form of cube. \tt R_{across \ diagonal = \frac{5r}{6}}
- \tt R_{face \ diagonal} = \frac{3r}{4}
- \tt R_{two \ adjacent \ corners} = \frac{7r}{12}
View the Topic in this video From 17:34 To 54:14
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. The equivalent resistance of the combination of resistors is
Rs = R1 + R2 + R3
2. The equivalent resistance of the combination of resistors is
\frac{1}{R_{p}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}
3. If n identical resistances are connected in series Req = nR and potential difference across each resistance is V = V/n
4. Current through any resistance is
\tt i = I_{total} \times \left[\frac{Resistance \ of \ opposite \ branch}{Total \ resistance}\right]

