Motion in a Straight Line
Understanding motion through graph
- Slope of position time graph given velocity.
- S-t graph of particle moving with uniform velocity.
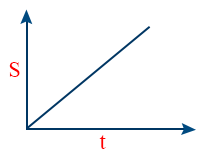
- S-t graph of particle moving with uniform acceleration
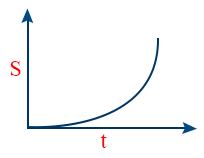
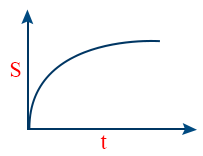
- S-t graph of particle moving with uniform retardation.
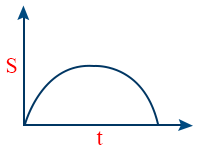
- S-t graph of particle projected up
- Slope of velocity time graph given acceleration.
- Area of velocity time graph given displacement.
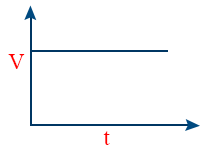
- V – t graph of particle moving with uniform velocity
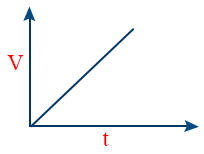
- V – t graph of particle moving with uniform acceleration
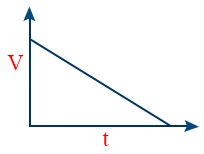
- V – t graph of particle moving with uniform Retardation
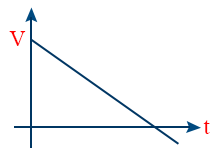
- V – t graph of particle projected up
- S - t graph of a particle at rest

- Area of acceleration time graph given change in velocity
- a – t graph of a freely falling body
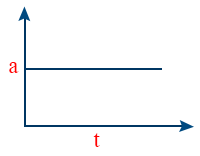
- a – t graph when acceleration is increasing and positive
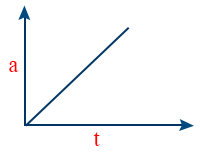
- a – t graph when acceleration is decreasing and Negative
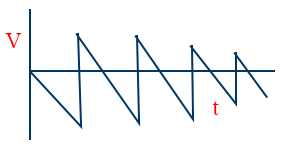
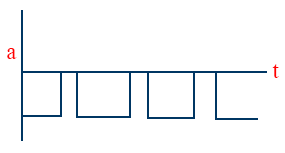
- V - t graph of a ball released from Certain height and taken certain bounces.
- S - t graph of a ball released from Certain height and taken certain bounces.
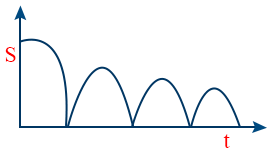
- a – t graph of a ball released from Certain height and taken certain bounces.
- Vt graph of a particle (α) accelerated for some time and (β) accelerated for same time
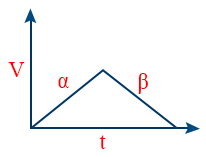
- Maximum velocity \tt V_{max}=\left(\frac{\alpha\beta}{\alpha+\beta}\right)\cdot t
Total displacement \tt S=\frac{1}{2}\left(\frac{\alpha\beta}{\alpha+\beta}\right)\cdot \ t^{2}
View the Topic in this video From 00:07 To 07:59
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.

