Motion in a Plane
Scalars and Vectors quantities
- A vector quantity is that which has both magnitude direction and satisfies laws of vector addition, a scalar quantity is that which has only magnitude.
- A unit vector is that which has 1 unit magnitude and a null vector is that which has O magnitude \hat{r} = \frac{\overline{r}}{|r|}
- A vector-quantity can be resolved in to any number of components when resolved in to two components Rx = R cos θ and Ry = R sin θ
- A vector resolved in to 3D space then the direction cosines as \cos \alpha = \frac{R_{x}}{|R|}, \cos \beta = \frac{R_{y}}{|R|}, \cos \gamma = \frac{R_{z}}{|R|} and cos2 α + cos2 β + cos2 γ = 1.
- Parallelogram law of vectors states that if two vectors are represented both in magnitude and direction by the two sides of a parallelogram from the same point then their resultant is represented by the diagonal passing through the same point both in magnitude and direction.
R = \sqrt{P^{2} + Q^{2} + 2 PQ \cos \theta} - Triangle law of vectors states that, if two vectors are represented in both magnitude and direction by the two sides of a triangle taken in order then their resultant is represented by the closing side of a triangle taken in the reverse order.
- The dot product of two vectors is the product of magnitudes of the vectors and cos of angle between them. \overline{a} \cdot \overline{b} = |a||b|\cos \theta Dot product is used to find the angle between the vectors.
- The cross product of two vectors is the product of magnitude of vectors and sin of angle between them. \overline{a} \times \overline{b} = |a||b|\sin \theta \cdot \hat{n}
- Cross product of two vectors is not commutative cross product obeys distributive \overline{A} \times \left(\overline{B} + \overline{C}\right) = \overline{A} \times \overline{B} + \overline{A} \times \overline{C} If vectors are parallel then cross product = 0
- Dot product of two vectors is Commutative Dot product obeys Destributive \overline{A} \cdot \left(\overline{B} + \overline{C}\right) = \overline{A} \cdot \overline{B} + \overline{A} \cdot \overline{C} If vectors are perpendicular the Dot product = 0
View the Topic in this video From 2:55 To 55:46
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. A unit vector in the direction of vector A is given by
\hat{A} = \frac{A}{A}
2. The displacement vector for AB is Δr = r2 − r1
3. Triangle Law of Vectors Addition: If two vectors A and B acting at a point are inclined at an angle θ, then their resultant
R = \sqrt{A^{2} + B^{2} + 2AB \cos \theta}
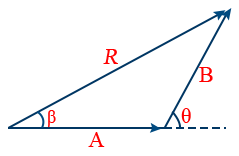
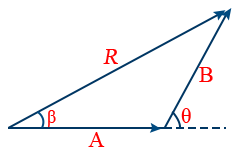
4. If the resultant vector R subtends an angle β with vector A, then
\tan \beta = \frac{B \sin \theta}{A + B \cos \theta}
5. Parallelogram Law of Vectors Addition: Resultant of vectors A and B is given by
R = \sqrt{A^{2} + B^{2} + 2AB \ \cos \ \theta}
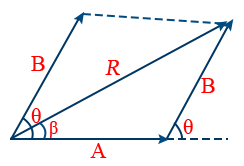
6. If the resultant vector R subtends an angle β with vector A, then
\tan \beta = \frac{B \sin \theta}{A + B \cos \theta}

7. Polygon Law of Vectors Addition: R = A + B + C + D + E
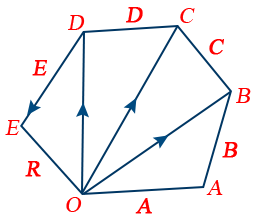
8. OE = OA + AB + BC + CD + DE
9. Properties of Vectors Addition:
(i) Vector addition is commutative, i.e. A + B = B + A
(ii) Vector addition is associative, i.e., A + (B + C) = B + (C + A) = C + (A + B)
(iii) Vector addition is distributive, i.e. m (A + B) = mA + mB
(iv) A + 0 = A
10. Resolution of Vectors into two Components: Suppose OP = λA and PQ = μB, where λ and μ are two real numbers.
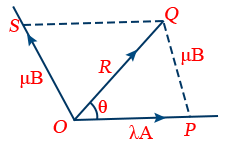
The resultant vector, R = λA + μB
11. Resolution of a Vector into Rectangular Components: Magnitude of vector A = \sqrt{A_{x}^{2} + A_{y}^{2}}
12. Direction Cosines of a Vector: cos2 α + cos2 β + cos2 γ = 1
13. Subtraction of Vectors: A − B = A + (−B)
14. Scalar or Dot Product of Two Vectors: A · B = AB cos θ
15. Properties of Scalar Product:
(i) Scalar product is commutative, i.e., A · B = B · A
(ii) Scalar product is distributive, i.e., A · (B + C) = A · B + A · C
(iii) Scalar product of two perpendicular vectors is zero A · B = AB cos 90° = 0
(iv) Scalar product of two parallel vectors or anti-parallel vectors is equal to the product of their magnitudes, i.e.
A · B = AB cos 0° = AB (for parallel)
A · B = AB cos 180° = −AB (for anti-parallel)
(v) Scalar product of a vector with itself is equal to the square of its magnitude, i.e. A · A = AA cos 0° = A2
(vi) Scalar product of orthogonal unit vectors
\tt \hat{i} \cdot \hat{i} = \hat{j} \cdot \hat{j} = \hat{k} \cdot \hat{k} = 1
and \tt \hat{i} \cdot \hat{j} = \hat{j} \cdot \hat{k} = \hat{k} \cdot \hat{i} = 0
(vii) Scalar product in cartesian coordinates
\tt A \cdot B = (A_{x} \hat{i} + A_{y} \hat{j} + A_{z} \hat{k}) \cdot (B_{x} \hat{i} + B_{y} \hat{j} + B_{z} \hat{k}) = A_{x}B_{x} + A_{y}B_{y} + A_{z}B_{z}
16. Vector or Cross Product of Two Vectors: \tt A \times B = AB \sin \theta \ \hat{n}
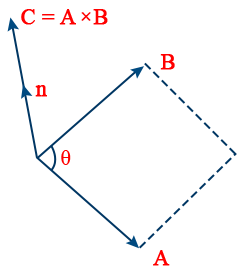
17. Properties of Vector Product:
(i) Vector product is not commutative, i.e. \tt A \times B \neq B \times A \ [\therefore (A \times B) = - (B \times A)]
(ii) Vector product is distributive, i.e. A × (B + C) = A × B + A × C
(iii) Vector product of two parallel vectors is zero, i.e., A × B = AB sin 0° = 0
(iv) Vector product of any vector with itself is zero. A × A = AA sin 0° = 0
(v) Vector product of orthogonal unit vectors
\tt \hat{i} \times \hat{i} = \hat{j} \times \hat{j} = \hat{k} \times \hat{k} = 0
and \tt \hat{i} \times \hat{j} = \hat{k}, \hat{j} \times \hat{k} = \hat{i}, \hat{k} \times \hat{i} = \hat{j}

