Motion in a Plane
Kinematics of Circular Motion
- The angle swept by the radius vector is called angular displacement the unit of angular displacement is radian.
- The angular velocity is the rate of change of angular displacement in unit time. The unit of angular velocity is radian per second W = dθ/dt
- The angular acceleration is the rate of change of angular velocity in unit time. The unit of angular acceleration is radian per second. ∝ = dw/dt
- The relation between Linear velocity and angular velocity is v = \overline{w} \times \overline{r} where \overline{r} is the position vector of the particle with respect to centre of circle.
- The relation between Linear acceleration and angular acceleration is \overline{a} = \overline{\alpha} \times \overline{r} where \overline{r} is the position vector of the particle with respect to centre of circle
- Tangential acceleration is the component of acceleration in the direction of velocity which is responsible for change in speed of particle (at = dv/dt) Thin component is tangential to the circle
- Radial acceleration is the component of acceleration in a direction towards centre. This component is responsible for change in direction of Velocity. a_{r} = \frac{v^{2}}{r} = rw^{2}
- The final angular velocity wf = wi + αt when α is the angular acceleration and 't' is the time and wi is the initial angular velocity.
- The final angular velocity wf2 = wi2 + 2 αθ where 'α' is the angular acceleration and 'θ' is the angular displacement.
- The angular displacement \theta = wit + \frac{1}{2} \alpha t^{2} where 'wi' is the initial angular velocity 'α' is the angular acceleration at time 't'.
View the Topic in this video From 20:29 To 29:33
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Angular displacement (Δθ) = \frac{\Delta s}{r}
2. Angular velocity (\omega) = \frac{\Delta \theta}{\Delta t}
3. Angular acceleration (\alpha) = \frac{d \omega}{dt} = \frac{d^{2}\theta}{dt^{2}}
4. Centripetal acceleration \alpha = \frac{v^{2}}{r} = r\omega^{2}
5. Centripetal force F = \frac{mv^{2}}{r} = mr\omega^{2}
6. Kinematical Equations in Circular Motion
(i) ω = ω0 + αt (ii) \theta = \omega_{0}t + \frac{1}{2}\alpha t^{2} (iii) \omega^{2} = \omega_{0}^{2} + 2\alpha \theta
7. The coefficient of friction (μs) between the road and tyres should be, \mu_{s} \geq \frac{v^{2}}{rg} \ {\tt or} \ v \leq \sqrt{\mu_{s} rg}
8. If centripetal force is obtained only by the banking of roads, then the speed (v) of the vehicle for a safe turn v = \sqrt{rg \tan \theta}
9. When centripetal force is obtained from friction force as well as banking of roads, then the maximum safe value of speed of vehicle
v_{max} = \sqrt{\frac{rg (\tan \theta + \mu)}{(1 - \mu \tan \theta)}}
10. If a cyclist inclined at an angle θ, then \tan \theta = \frac{v^{2}}{rg}
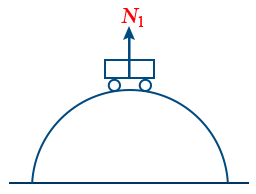
11. When a vehicle is moving over a convex bridge, then at the maximum height, reaction (N1) is
N_{1} = mg - \frac{mv^{2}}{r}
12. When a vehicle is moving over a concave bridge, then at the lowest point, reaction (N2) is
N_{2} = mg + \frac{mv^{2}}{r}

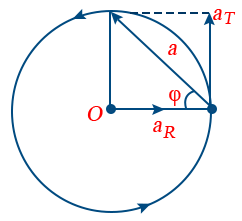
13. Both acceleration acts perpendicular to each other. Resultant acceleration
a = \sqrt{a_{R}^{2} + a_{T}^{2}} = \sqrt{\left[\frac{v^{2}}{r}\right]^{2} + (r\alpha)^{2}}
and \tan \phi = \frac{a_{T}}{a_{R}} = \frac{r^{2}\alpha}{v^{2}}
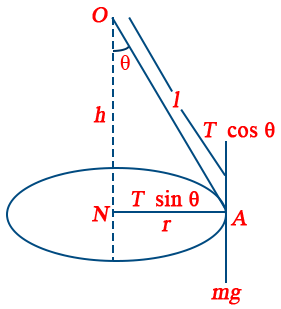
14. Time period of conical pendulum, T = 2\pi\sqrt{\frac{l \cos \theta}{g}}