Laws of Motion
Second Law of Motion: Momentum and Impulse
- According to second law of motion the rate of change of linear momentum is directly proportional to the external force applied on it.
- Newton’s second law of motion gives the formula of force f = ma.
- Second law implies that when a bigger force is applied on a body its linear momentum changes fast.
- Linear momentum is defined as the product of mass and velocity P = mv.
- Momentum in a vector quantity.
- Relation between F and P is \tt F \propto \frac{dp}{dt}
- 1 Newton = 105 dynes.
- \tt F = \frac{m(v - u)}{t} where, v = final velocity, u = inertial velocity.
- If “v” is constant and ‘m’ is changing \tt F = V\frac{dm}{dt}
- \tt F = \frac{P_{2} - P_{1}}{t} where, P1 = initial momentum, P2 = final momentum
- When a large force is acting on a small internal of time the product of force and time is called Impulse (J).
- The impulse J = f(t) = ∫fdt is a quantity that combines the net force and the time interval over which the force acts.
- Area under force time graph gives impulse.
- If a gun fires n bullets of mass ‘m’ \tt F = \frac{nmv}{t}
- If water of density ‘ρ’ coming out of pipe of area of cross section A with speed ‘v’ F = Aρv2
- The reaction force on a person in a lift moving up with acceleration R = m (g + a)
- The reaction force on a person in a lift moving down with deceleration R = m (g + a)
- The reaction force on a person in a lift moving up deceleration R = m (g − a)
- The reaction force on a person in a lift moving down acceleration R = m (g − a)
- The reaction force on a person in a freely falling lift R = 0.
- The force on between two bodies at contact is called contact force.
- Contact force \tt F = \frac{M_{2} F}{M_{1} + M_{2}}

- Acceleration of two bodies system \tt a = \frac{F}{M_{1} + M_{2}}
- For three bodies \tt a = \frac{F}{m_{1} + m_{2} + m_{3}}

- Tension is an electromagnetic force in a string due to force.
- Acceleration of two bodies connected by string \tt a = \frac{F}{m_{1} + m_{2}}
- Tension in string \tt T = \frac{m_{2} F}{m_{1} + m_{2}}
- Acceleration of three bodies connected by string \tt a = \frac{F}{m_{1} + m_{2} + m_{3}}
- Tension in first string \tt T_{1} = \frac{m_{1} F}{m_{1} + m_{2} + m_{3}}
- Tension in second string \tt T_{2} = \frac{\left(m_{1} + m_{2}\right) F}{m_{1} + m_{2} + m_{3}}
- At woods machine acceleration \tt a = \frac{m_{1} - m_{2}}{m_{1} + m_{2}} g
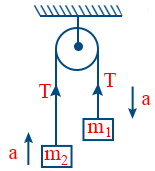
- Tension \tt T = \frac{2 m_{1}m_{2}}{m_{1} + m_{2}} \cdot g
- Thrust on the pulley = \tt 2T = \frac{4 m_{1}m_{2} g}{m_{1} + m_{2}}
- Acceleration \tt a = \frac{m_{1} g}{m_{1} + m_{2}}
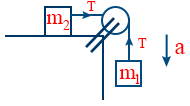
- Tension in string \tt T = \frac{m_{1} m_{2} g}{m_{1} + m_{2}}
- Acceleration \tt a = \frac{\left(m_{1} - m_{2} \sin \theta \right) g}{m_{1} + m_{2}}
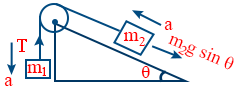
- Tension \tt T = \frac{m_{1} m_{2} \left(1 + \sin \theta \right)}{m_{1} + m_{2}}
- Acceleration \tt a = \frac{\left(m_{1} \sin \alpha - m_{2} \sin \beta \right) g}{m_{1} + m_{2}}
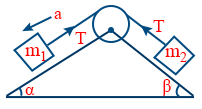
- Tension \tt T = \frac{m_{1} m_{2} \left(\sin \alpha + \sin \beta \right) g}{m_{1} + m_{2}}
View the Topic in this video From 0:36 To 44:05
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Newton's Second Law of Motion: \tt F = \frac{mdv}{dt} = ma
2. Impulse = Force × Time = Change in momentum
3. Position dependent force: Gravitational force between two bodies \frac{Gm_{1}m_{2}}{r^{2}}

