Laws of Motion
Conservation of Momentum, Equilibrium of a Particle and friction
- When no external forces are acting on the system the total momentum of the system remains constant.
- Total momentum of system before collision is equal to the total momentum of system after collision.
- When two objects exert forces on each other in action reaction, their motions are affected as a pair m1v1 + m2v2 = 0
- Recoil velocity of gun is \tt v_{g} = -\frac{-m_{b} v_{b}}{M_{g}}
- Change in momentum ΔP = mv – mu.
- Resultant momentum \tt \Delta P = \sqrt{P_{1}^{2} + P_{2}^{2} + 2P_{1}P_{2} \cos \theta}
- Change in momentum in opposite direction ΔP = m(v + u).
- A ball hits wall with “u” at an angle “θ” with normal to wall ΔP = 2 mu cos θ.
- Change in momentum along wall = 0.
Friction:
- The frictional force acting between two surfaces at rest with respect to each other is called static friction fs = μs N.
- The frictional force between surfaces in motion is called Kinetic friction fK = μK N.
- The frictional force when rolls over, the surface of another called Rolling friction fR = μR N.
- The cofficient of friction μ is fs > fK > fR μs > μK > μR .
- The angle between net contact force and Normal reaction called angle of friction tan θ = fs/N.
- Acceleration of body moving over rough surface \tt a = \frac{F- \mu_k \mu_g}{M}
- Frictional force on a block of mass ‘M’ when a pushing force “F” is applied making an angle ‘θ’ with horizontal F = μ (μg − F sin θ)
- Minimum force acquired to pull \tt F = \frac{- \mu m g}{\cos \theta + \mu \sin \theta}
- Frictional force on a block of mass M when a pushing force ‘F’ is applied making an angle ‘θ’ with horizontal F = μ (μg + F sin θ)
- Minimum force required to pull \tt F = \frac{\mu m g}{\cos \theta - \mu \sin \theta}
- Acceleration of block pressed to vertical wall \tt a = \frac{Mg - f_{k}}{m}
- Block of mass ‘m’ kept on truck moving with aτ (acceleration) acceleration of block \tt a_{B} = \frac{ma_{\tau} - f_{k}}{m}
- Velocity of block \tt v = \sqrt{2 (a_{\tau} - \mu k g) x}
- Time taken to move \tt t = \sqrt{\frac{2x}{\left(a_{\tau} - \mu k g\right)}}
- Acceleration of block of a smooth incline a = g sin θ
- Time taken to reach bottom t = \tt \sqrt{\frac{2 l}{g \sin \theta}}
- Velocity of block at bottom \tt v = \sqrt{2 g l \sin \theta}
- Acceleration of block on rough inclined plane a = g (sin θ – μK cos θ)
- Velocity of block to reach bottom \tt v = \sqrt{2 g l (\sin \theta - \mu k \cos \theta)}
- Time taken to reach bottom \tt t = \sqrt{\frac{2 l}{g (\sin \theta - \mu k \cos \theta)}}
- Force required to move the block up the plane F = mg (sin θ + μK cos θ).
- When the body thrown up with velocity “U” The retarding force F = mg (sin θ + μK cos θ).
- The retardation a = g (sin θ + μK cos θ)
- Time taken to stop \tt t = \sqrt{\frac{2 l}{g (\sin \theta + \mu k \cos \theta)}}
- Distance travelled by body to stop \tt s = \frac{u^{2}}{2 g (\sin \theta + \mu k \cos \theta)}
- Acceleration of system of two Blocks when Force is applied on Bottom block amax = μs g.
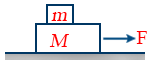
- Maximum force for which blocks move together Fmax = μs (M+m)g
- Acceleration of Lower block \tt a = \frac{F - \mu k mg}{M}
- Acceleration of system of two blocks when force is applied on top block \tt a = \frac{\mu s mg}{M}
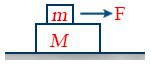
- Maximum force for which both blocks move together \tt F = (M + m) \frac{\mu s mg}{M}
- Acceleration of lower block = \tt \frac{\mu_k mg}{M}
- Acceleration of upper block = \tt \frac{F - \mu_k mg}{m}
View the Topic in this video From 0:03 To 08:03
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. According to this law of conservation of linear momentum for a system of particles \overrightarrow{F} = \frac{d\overrightarrow{p}}{dt}
2. If two forces F1 & F2 act an a particle then they will be in equilibrium \therefore \ \overrightarrow{F_{2}} = -\overrightarrow{F_{1}}
3. Recoil velocity of gun \overrightarrow{v}_{G} = - \frac{m_{B}}{m_{G}}{\overrightarrow{v}_{B}}
4. If 'n' bullets each of mass m are fired per unit time from a machine gun, then the force required to hold the gun \tt = v \left[\frac{dm}{dt}\right] = v (mn) = mnv.
5. Thrust on the rocket : F = -u \frac{dm}{dt}
6. Acceleration of the rocket : \tt a = \frac{u}{m} \frac{dm}{dt} -g
7. Instantaneous velocity of the rocket :\tt v = u \log_{e}\left[\frac{m_{0}}{m}\right] - gt
8. Burnt out speed of the rocket : \tt v_{b} = v_{max} = u\log_{e}\left[\frac{m_{0}}{m_{r}}\right]
9. Weight (W) → w = mg
10. When a lift is at rest or moving with a constant speed, then R = mg
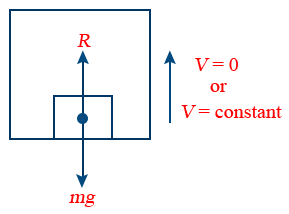
11. When a lift is accelerating upward, then apparent weight R1 = m(g + a)

12. When a lift is accelerating downward, then apparent weight R2 = m(g − a)
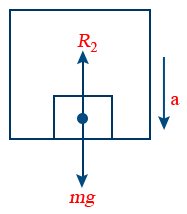
13. When lift is falling freely under gravity, then R2 = m(g − g) = 0
14. Minimum force required to move the body up the inclined plane ƒ1 = mg (sin θ + μ cos θ)
15. Minimum force required to push the body down the inclined plane ƒ1 = mg (μ cos θ − sin θ)
16. Two Bodies in Contact:
Acceleration of the bodies a = \frac{F}{(m_{1} + m_{2})}
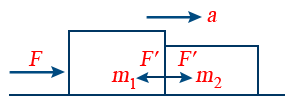
Contact force on m_{1} = m_{1}a = \frac{m_{1}F}{(m_{1} + m_{2})}
Contact force on m_{2} = m_{2}a = \frac{m_{2}F}{(m_{1} + m_{2})}
17. Three Bodies in Contact:
Acceleration of the bodies = \frac{F}{(m_{1} + m_{2} + m_{3})}
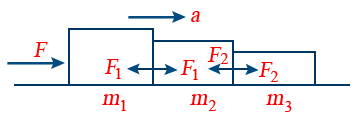
Contact force between m1 and m2 → F_{1} = \frac{(m_{2} + m_{3})F}{(m_{1} + m_{2} + m_{3})}
Contact force between m2 and m3 → F_{2} = \frac{m_{3}F}{(m_{1} + m_{2} + m_{3})}
18. Motion of Two Bodies, One Resting on the Other:
Acceleration of two bodies
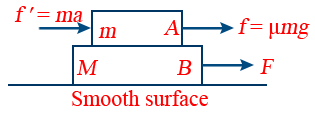
a = \frac{F}{(M + m)}
Pseudo force acting on block B due to the accelerated motion ƒ' = ma
19. Motion of Bodies Connected by strings:

Acceleration of the system a = \frac{F}{(m_{1} + m_{2} + m_{3})}
Tension in string T1 = F
T_{2} = (m_{2} + m_{3})a = \frac{(m_{2} + m_{3})F}{(m_{1} + m_{2} + m_{3})}
T_{3} = m_{3}a = \frac{m_{3}F}{(m_{1} + m_{2} + m_{3})}
20. Pulley Mass System:
When unequal masses m1 and m2 are suspended from a pulley (m1 > m2)

a = \frac{(m_{1} - m_{2})}{(m_{1} + m_{2})}g
T = \frac{2m_{1}m_{2}}{(m_{1} + m_{2})}g

