Moving charges and magnetism
Moving Coil Galvanometer
- Current in MCG \tt i = \frac{C \theta}{BAN}
- Current sensitivity \tt Si = \frac{BAN}{C}
- Voltage sensitivity \tt SV = \frac{\theta}{iG} = \frac{BAN}{CG}
- MCG can measure current up to 10−9 Amp.
- Shunt is a low resistance connected in parallel to galvanometer to protect from large current.
- R Equivalent = \tt \frac{GS}{G + S}
G = Galvanometer resistance , S = Shunt resistance - V = iReq = \tt i \frac{GS}{G+S}
- V = ig G = is S.
- Ammeter is an instrument used to measure current
- Shunt resistance \tt S = \frac{G}{\left(\frac{i}{ig} - 1\right)}
- Ammeter must always be connected in series in the circuit.
- Galvanometer can be converted in to Ammeter by connecting a shunt in parallel.
- Galvanometer can be converted in to voltmeter by connecting high resistance in series.
- V = ig (G + R)
- Voltmeter is used to measure potential difference across the elements in the circuit.
- Resistance of a voltmeter is very high.
- Among low range and high range voltmeter high range voltmeter has more resistance.
- Equivalent resistance of voltmeter = G + R
- Resistance to be connected in series \tt R = \frac{V}{ig} - G
- Tangent galvanometer works on the principle of B = BH Tanθ
- Magnetic induction at the centre of loop = \tt \frac{\mu_0ni}{2r}
- \tt i=\left(\frac{2rB_H}{\mu_0n}\right)\tan \theta
- Reduction factor \tt K=\left(\frac{2rB_H}{\mu_0n}\right)
- Tangent galvanometer cannot be used at magnetic poles
- Tangent galvanometer can measure current upto 10−6 A
- Magnetic moment of a current of length L wire bent in the form of a circle is \tt \frac{iL^2}{4\pi}
- Magnetic field at the centre of loop is \tt B=\left(\frac{\pi -\theta}{\pi}\right)\frac{\mu_0i}{2a}
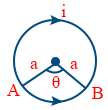
- Magnetic field at the centre \tt B=\frac{\mu_0i}{2\pi r}\left(\pi -\phi+\tan\phi\right)
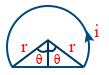
- Magnetic induction at point o \tt B=\frac{\mu_0i}{4r}\left[\frac{3}{2}-\frac{1}{\pi}\right]
- Cyclotron is a machine to accelerate charged particles.
- Principle of cyclotron is frequency of revolution of charged particle in a magnetic field is independent of its energy.
- Centripetal force in cyclotron \tt F=\frac{mv^2}{r}=Bqv
- Radius of circular path \tt r=\frac{mv}{Bq}
- Time period of charged particle \tt T=\frac{2\pi m}{Bq}
- Frequency of charged particle \tt f=\frac{Bq}{2\pi m}
- KE of charged particle =\tt \frac{1}{2}\frac{B^2q^2r^2}{m}
- Use Amperes Right hand grip rule to find the direction of magnetic lines of force around current carrying conductor.
- Use Fleming's left hand rule to know the direction of O force when charge particle moving in magnetic field.
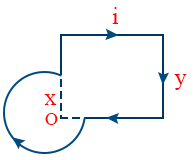
- Magnetic field at p is zero.
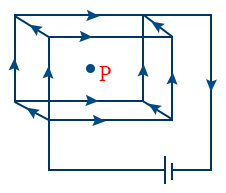
- The net force at O is zero.

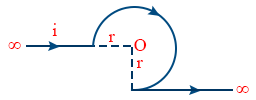
- Magnetic field induction at 'O' is \tt B=\frac{\mu_0i}{4\pi}\left(\frac{3\pi}{4x}+\frac{\sqrt 2}{2y}\right)
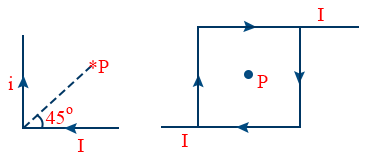
- Magnetic induction at p is \tt B=\frac{\mu_0i}{2\pi r}\left(1+\sqrt2\right)
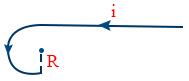
- Magnetic induction at 'O' is\tt B=\frac{\mu_0}{4\pi}\frac{i}{R}\left(\pi +1\right)
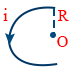
- Magnetic induction at O is \tt B=\frac{\mu_0i}{2r}\left(\frac{\pi}{2\pi}\right)=\frac{\mu_0i}{4r}
View the Topic in this video From 02:15 To 20:53
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. In moving coil galvanometer the current I passing through the galvanometer is directly proportional to its deflection (θ).
I ∝ θ or, I = Gθ
where G = \frac{k}{NAB} = galvanometer constant
2. Current sensitivity : It is defined as the deflection produced in the galvanometer, when unit current flows through it.
I_{s} = \frac{\theta}{I} = \frac{NAB}{k}
3. Voltage sensitivity : It is defined as the deflection produced in the galvanometer when a unit voltage is applied across the two terminals of the galvanometer
V_{s} = \frac{\theta}{V} = \frac{\theta}{IR} = \frac{NAB}{kR}

