Alternating Current
AC Voltage Applied to a Resistor and Phasors
- If the current in a circuit changes its direction in every \tt \frac{T}{2} sec then the current is called ALTERNATING CURRENT (ac)
- The emf of a source which produces sinusoidally varying potential difference across its terminals is given as, e = eo sin wt
- The average current over a complete cycle is ZERO
- For symmetric waves, the average value for half cycle is measured
- \tt i_{ave}=\frac{2}{\pi}\ i_{0}=0.637\ i_{0}
- \tt e_{ave}=\frac{2}{\pi}\ e_{0}=0.637\ e_{0}
- \tt i_{rms}=\frac{i_{0}}{\sqrt{2}}\ i_{0}=0.707\ i_{0}
- \tt e_{rms}=\frac{e_{0}}{\sqrt{2}}\ i_{0}=0.707\ e_{0}
- If a d.c ammeter is connected to an a.c source then the reading is shown as zero.
- It is important to measure and specify rms values for a.c quantities .
- When a resistor is connected to an a.c source, the average power loss (P) \tt P=V_{rms}^2/R\ or\ P=I_{rms}V_{rms\ }\ or\ P=I_{rms}^2\ R
- Analogous value for resistance for an ideal inductor is LW. It is called Inductive reactance (XL)
- Analogous value for resistance for a capacitor is 1/CW. It is called capacitive reactance, XC.
- The REACTANCE is the total resistance offered by the circuit due to capacitor and inductor. It is equal to \tt X_{L}\sim X_{C}
- The total Resistance a circuit offers is called IMPEDENCE, Z.
\tt Z=\sqrt{\left(X_{L}-X_{C}\right)^2+R^{2}} - VOLTAGE LEAD and CURRENT LEAD are the two phasor diagrams for LCR series circuits.
-
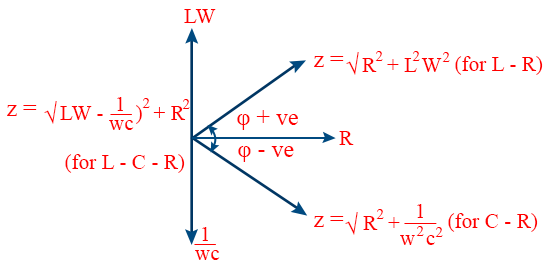
- The peak current is given by \tt i_{0}=\frac{e_{0}}{Z} for AC voltage applied to inductor.
- The impedence is given by Z = LW (Pure inductor)
- The Phase difference between emf and current is given by the relation \tt \phi=\tan^{-1}\frac{\omega L}{Q}\Rightarrow\phi=\frac{\pi}{2}
- The instantaneous alternating current, i = io sin (wt + φ) when AC voltage is applied to the capacitor.
- The maximum current when AC voltage is applied to the capacitor is given by \tt i_{0}=\frac{e_{0}}{Z}
- The impedence when AC voltage is applied to capacitor is given by
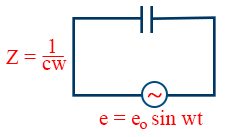
- When AC voltage is applied to capacitor, then the phase difference between emf and current is given by \tt \phi=\tan^{-1}\frac{1/c\omega }{0}\Rightarrow\phi=\frac{\pi}{2}
- When AC voltage is applied across L – R, the instantaneous alternating current is given as i = io sin (wt - φ)
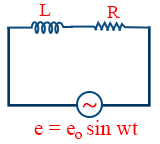
- When AC voltage is applied across L – R , the maximum current is \tt i_{0}=\frac{e_{0}}{Z}
- When AC voltage is applied across L – R, the impedance is \tt Z=\sqrt{R^{2}+L^{2}\omega^{2}}
- AC voltage is applied across L – R, then the phase difference between emf and current is \tt \phi=\tan^{-1}\frac{L\omega}{R}
- AC voltage applied across R – C series, then the instantaneous alternating current is, i = io sin (wt + φ)
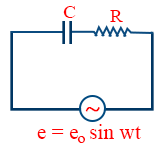
- AC voltage applied across R – C series, then the maximum current, \tt i_{0}=\frac{e_{0}}{Z}
View the Topic in this video From 00:24 To 10:43
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. The instantaneous value of alternating current at any instant of time t is given by
I = I0 sin ωt
where, I0 = peak value of alternating current.
2. Mean or average value of alternating current for first half cycle
I_{m} = \frac{2I_{0}}{\pi} = 0.637 I_{0}
3. Root mean square value of alternating current
I_{v} = I_{rms} = \frac{I_{0}}{\sqrt{2}} = 0.707 I_{0}
4.Root mean square value of alternating voltage
V_{rms} = \frac{V_{0}}{\sqrt{2}} = 0.707 V_{0}
5. Total resistance of a circuit offer Impedance of an AC circuit, Z = \sqrt{R^{2} + (X_{L} - X_{C})^{2}}
6. The average power in an AC circuit,
P_{av} = V_{rms} \ i_{rms} \ \cos \theta

