Relations and Functions
Composition of Functions and Invertible Function
- Composite function: If f and g are two functions, then the composite function f and g is denoted by gof and it is defined only when codomain of f equal to domain of g. i.e.
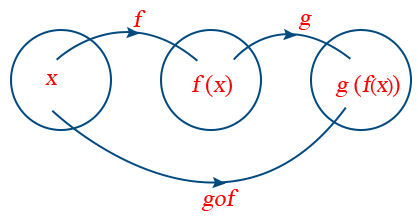
- If f : A → B and g : B → C are two functions, then the composite function gof : A → C is defined as gof(x) = g[f(x)] ∀ x ∈ A.
- If f and g are two bijective functions then gof is also bijective.
- If gof is one one, then f is one one but g may not be one one.
- If gof is onto, then g is onto but f may not be onto.
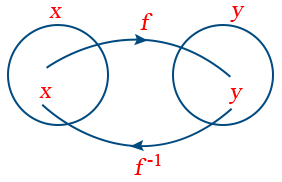
- Inverse of a function: If the function f : x → y is bijective, then we defined inverse of f as f−1 : y → x by the rule y = f(x) ⇔ x = f−1 (y) ∀ x ∈ X, y ∈ Y.
- If f : A → B and g : B → C are two bijective functions then (gof)−1 = f−1og−1
- The graph of y = f(x) and y = f−1(x) intersects on the line y = x i.e the solution of f(x) = f−1(x) is solution of y = x
- Even and odd function: A function f(x) is said to be f(−x) = f(x) then it even function.
A function f(x) is said to be f(−x) = −f(x), then it is odd function. - Every function f(x) can be express as sum of even and odd functions. ie f(x)=\frac{f(x)+f(-x)}{2}+\frac{f(x)-f(-x)}{2}
- The graph of even function is symmetric about the y-axis.
- The graph of odd function is symmetric about the origin and is placed in first and third quadrant (or) second and fourth quadrants.
- If f(x) is even function, then f'(x) is odd function provided f'(x) is defined on R.
- If f(x) is odd function, then f'(x) is even function provided f'(x) is defined on R.
1.
| f | g | fog | gof |
| Even | Even | Even | Even |
| Even | Odd | Even | Even |
| Odd | Even | Even | Even |
| Odd | Odd | Odd | Odd |
2. E = Even function, O = Odd function, N = Neither even nor odd function
| E + E = E | E − E = E | O − O = O |
| E E = E | O + O = O | E − O = O − E = N |
| O O = E | \frac{E}{E}=E | En = E |
| E O = O E = O | \frac{O}{E}=\frac{E}{O}=O \frac{O}{O}=E |
O^{n}=\begin{cases} O &\tt n \ is \ odd\\E & \tt n \ \ is \ even\end{cases} |
- All even functions are many one.
- Even extension: The even extension is obtained by defining a new function g(x) as
g(x)=\begin{cases}f(x) & x \in [0, a]\\f(-x) & x \in [-a, 0]\end{cases} - Odd extension: The odd entension is obtained by defining a new function g(x) as
g(x)=\begin{cases}f(x) & x \in [0, a]\\-f(-x) & x \in [-a, 0]\end{cases} - If f : A → B is a bijection, then f−1 : B → A is also a bijective function.
- If f : A → B is a bijection, then (f−1)−1 = f
- The inversion of a bijection is unique
- If f : A → B is a bijection then f−1of = IA and fof−1 = IB.
- If f : A → B is a bijection if and only if there exists a function g : B → A such that gof = IA.
View the Topic in this video From 20:35 To 55:26
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
- If f : A → B and g : B → C are two function then the composite function of f and g, gof A → C will be defined as gof(x) = g[f(x)], ∀ x ∈ A
- Composite of functions is not commutative i.e., fog ≠ gof.
- Composite of functions is associative i.e., (fog)oh = fo(goh).
- If f : A → B and g : B → C are two bijections, then gof : A → C is bijection and (gof)−1 = (f−1og−1).
- fog ≠ gof but if, fog = gof then either f−1 = g or g−1 = f also, (fog)(x) = (gof)(x) = (x).
- (f−1)−1 = f
- If f and g are two bijections such that (gof) exists then (gof)−1 = f−1og−1.

