Solid State
Packing Efficiency, Close Packed Structures and Voids
- Close pack structures:
- 1-dimension close pack structure: Points cling together in a line as shown below.

- Co-ordination number: Number of nearest neighbouring points around a point is called co-ordination number.
- Co-ordination number of 1-D close pack is 2
- 2-D close pack are of two types (a) 2 - D square close pack (b) 2 - D hexagonal close pack
- 2-D square close pack as shown below
- <

- 2 - D. A A A ..... arrangement is called 2-D square close pack.
- Co-ordination number of 2-D square close pack is 4.
- 2D-Hexagonal close pack is obtained by placing 1D-One layer over constriction of another 1-D layer.

- Co-ordination number of 2-D Hexagonal close pack is 6.
- Void: The empty space in close pack is called void.
- There are 2 types of voids in 2D close pack
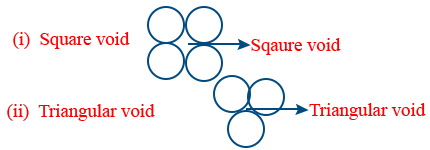
- Square void is in 2D-square close pack; Triangular void in 2D-Hexagonal close pack.
- 3D-close pack structures obtained by arrangement of one 2D layer over the other. In this we can get simple cubic, body centered, face centered (Cubic close pack), and Hexagonal close pack lattices.
- Simple cubic close pack can be obtained by placing one 2D-square close pack over the other each layer is identical. That is why this arrangement is also represented as 3D AAAA ......
- Body centered cubic crystal can also obtained by placing atoms of second layer on alternative square voids and third layer repeats as 1st layer.
So 3D obtained by ABAB .... square close pack arrangement is called B.C.C. - Arrangement of second layer over the first layer of 2D Hexagonal close pack leads two types of voids called "tetrahedral void", "Octahedral void"
- Tetrahedral void: An atom of above layer or below layer caps the triangular void of 2D- Hexagonal close pack forms tetrahedral void

- Octahedral void: The triangular voids in the second layer are above the triangular voids in the first layer, and these do not overlap. One of them has the apex of the triangle pointing upwards and the other downwards is called octahedral voids

- In any close pack if "N" number of atoms (or) spheres are present.
∴ The number of octahedral voids in it = N
The number of Tetrahedral voids in it = 2N - F.C.C (or) C.C.P close pack: If third layer placed by covering octahedral voids forms F.C.C (or) C.C.P structure.
- F.C.C (or) C.C.P close pack can be represented as ABCABC....
- Hexagonal close pack: This is obtained by arrangement of 3rd layer by covering tetrahedral voids and it is identical with first layer.
- H.C.P. can be represented as ABABAB....
- Co-ordination number of simple cubic is "6"
- Co-ordination number of B.C.C is "8"
- Co-ordination number of F.C.C, C.C.P and H.C.P is 12.
- Relations between voids and coordination number.
| Sl.No. | Name of void | rvoid/rsphere | Co-ordination number |
| 1. | Triangular void | 0.155 | 3 |
| 2. | Tetrahedral void | 0.225 | 4 |
| 3. | Octahedral void | 0.414 | 6 |
| 4. | Cubic void | 0.732 | 8 |
- Packing efficiency: It is the percentage of total space occupied by all the atoms present in unit cell.
- Packing efficiency can be calculated by using following formula = P.E = \frac{Volume\ occupied\ by\ all\ the\ atoms\ unit\ cell}{Volume\ of\ unit\ cell}\times100
- Trick for P.E is P.E = \frac{Z\times\frac{4}{3}\pi r^{3}}{a^{3}}\times100
- P.E for simple cubic = \frac{1\times\frac{4}{3}\pi r^{3}}{a^{3}}\times100
= \frac{1\times\frac{4}{3}\pi r^{3}}{(2r)^{3}}\times100
= 52.4% - P.E for B.C.C = \frac{2\times\frac{4}{3}\pi r^{3}}{a^{3}}\times100= \frac{2\times\frac{4}{3}\pi r^{3}}{\left(\frac{4r}{\sqrt{3}}\right)^{3}}\times100 = 68%
- P.E for F.C.C = \frac{4\times\frac{4}{3}\pi r^{3}}{a^{3}}\times100= \frac{4\times\frac{4}{3}\pi r^{3}}{\left(2\sqrt{2}\ r\right)^{3}}\times100 = 74%
- For H.C.P
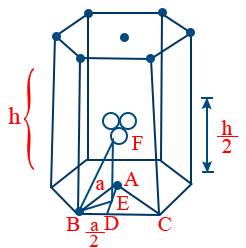
- Δ ABD
AB2 = AD2 + BD2
AD2 = AB2 − BD2
AD=\sqrt{a^{2}-\frac{a^{2}}{4}}=\frac{\sqrt{3}}{2} \ a=\frac{\sqrt{3}}{2} \ 2r=\sqrt{3}r - Δ BDE
\cos 30^{o}=\frac{a/2}{B.E}
B.E=\frac{a}{\sqrt{3}} - Δ ABC
Area =\frac{1}{2} \ Base \times height=\frac{1}{2} a \times\frac{\sqrt{3}}{2}a=\frac{1}{2}(2r)\frac{\sqrt{3}}{2}(2r)
Base area = =6\times \frac{1}{2}2r\frac{\sqrt{3}}{2}\times 2r=6\sqrt{3}r^{2} - Δ BDF
BF2 = BE2 + EF2
EF=\sqrt{BF^{2}-BE^{2}}=\sqrt{a^{2}-\frac{a^{2}}{3}}
\frac{h}{2}=a\sqrt{\frac{2}{3}}
h=2a\sqrt{\frac{2}{3}}
h=4r\sqrt{\frac{2}{3}}
Volume = Base × height =\left(6\sqrt{3}r^{2}\right)4r\sqrt{\frac{2}{3}}=24\sqrt{2}r^{3}
P.E=\frac{6\times\frac{4}{3}\pi r^{3}}{24\sqrt{2}r^{3}} = 74% - Location of tetrahedral voids in F.C.C:
- In F.C.C there are "8" tetrahedral voids
- Each tetrahedral void is located at \frac{1}{4}th distance from corner on body diagonal
- The distance between two tetrahedral voids in F.C.C is \frac{1}{2} × length of body diagonal.
- ∴ Distance between "2" tetrahedral voids on body diagonal is = \frac{1}{2}\sqrt{3}a=\frac{\sqrt{3}}{2}a
- In terms of radius of atom = \frac{\sqrt{3}}{2}(2\sqrt{2}r)=\sqrt{6}r
Part1: View the Topic in this Video from 0:09 to 21:45
Part2: View the Topic in this Video from 0:09 to 9:58
Part3: View the Topic in this Video from 0:09 to 6:43
Part4: View the Topic in this Video from 0:08 to 16:48
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. rvoid = 0.225 × rsphere (for tetrahedral voids)
2. rvoid = 0.414 × rsphere (for octahedral voids)

