Chemical Kinetics
Rate of a chemical reaction
Rate of reaction:
The change in concentration of a reactant or a product in unit time is called rate of reaction. Its unit is mole L−1 sec−1 (or) mol dm−3 sec−1 for solutions and kPa sec−1 or Nm−2 sec−1 for gases.
For example aA → bB
(i) Average rate of reaction = \tt \frac{-1}{a}\frac{\Delta \left[A\right]}{\Delta t}=\frac{1}{b}\frac{\Delta \left[B\right]}{\Delta t}
(ii) \tt -\frac{\Delta \left[A\right]}{\Delta t}\ and\ +\frac{\Delta \left[B\right]}{\Delta t} are average rate of consumption of A and average rate of production of B respectively.
(iii) −Δ[A] is decrease in concentration of A and +Δ[B] is increase in concentration of B in time taken Δt.
Instantaneous rate of reaction is the change in concentration of a reactant or a product at a given time.
It can be identified graphically only
For example w.r.t "A"
Instantaneous rate of reaction
\tt \lim_{\Delta t \rightarrow 0}\frac{\Delta \left[A\right]}{\Delta t}=-\frac{dx}{dt}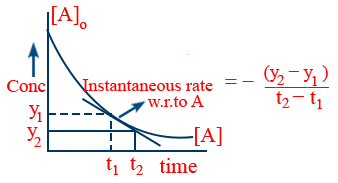
dx is very small change of concentration in very small change of time dt.
The kinetics of reaction can be followed (i.e., order, rate constant etc, can be established) by measuring a property which changes with time.
eg: (i) Total pressure in a gaseous reaction.
(ii) Volume of a reagent (Acidic Basic, oxidising or reducing agent)
(iii) Volume of a gaseous mixture (V)
(iv) Optical rotation (r)
For a reaction A0 → nB
| t = 0 | c | 0 |
| t = t | c − x | nx |
| t = ∞ | 0 | nc |
For any measurable property X proportional to the concentration of reaction mixture at various times, in terms of
(i) x0 and x
\tt k=\frac{1}{t}\ ln\ \frac{x_0}{x_0-x}
(ii) x0 and xt
\tt k=\frac{1}{t}\ ln\ \frac{x_0\left(n-1\right)}{nx_0-x_t}
(iii) x∞ and xt
\tt k=\frac{1}{t}\ ln\ \frac{\left(n-1\right)x_\infty}{n\left(x_\infty-x_t\right)}
(iv) x0, xt and x∞
\tt k=\frac{1}{t}\ ln\ \left(\frac{x_\infty-x_0}{X_\infty-x_t}\right)
x = amount of reacted in time t.
x0 = measured property at t = 0
xt = measured property at t = t
x∞ = measured property at t = ∞
Part1: View the Topic in this Video from 1:10 to 50:09
Part2: View the Topic in this Video from 33:00 to 39:06
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. For the reaction aA + bB → cC + dD
Rate of disappearance of a reactant is negative
\tt -\frac{d\left[A\right]}{dt} = Rate of disappearance of A
\tt -\frac{d\left[B\right]}{dt}= Rate of disappearance of B
Rate of formation of a product is positive
\tt \frac{d\left[C\right]}{dt}= Rate of formation of C
\tt \frac{d\left[D\right]}{dt}= Rate of formation of D
2. In terms of stoichiometric coefficient rate may be expressed as
\tt \frac{dx}{dt}=-\frac{1}{a}\frac{d\left[A\right]}{dt}=-\frac{1}{b}\frac{d\left[B\right]}{dt}=\frac{1}{c}\frac{d\left[C\right]}{dt}=\frac{1}{d}\frac{d\left[D\right]}{dt}
3. Rate in atm time-1 = Rate in mole L-1 time-1 × RT

