Organic Chemistry: Some basic Principles and Techniques
Isomerism, Homologous Series
Isomerism:
Iso = same, mer = parts (repeating)
Molecules which are having same molecular formula but different physical and chemical properties are called Isomers.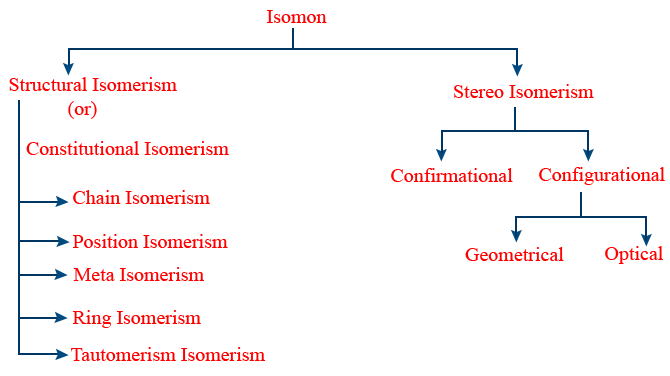
Structural Isomerism:
Differ in their structures are called structural Isomers, and the phenomena is called structural Isomerism.
Linkage of atoms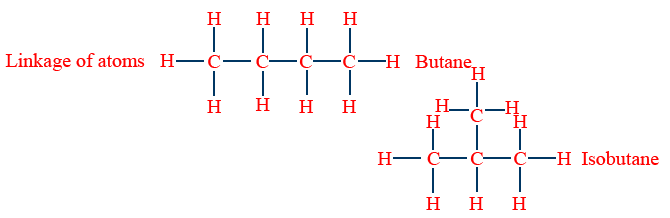
Chain Isomerism:
Isomers which differ in their carbon chains are called chain Isomers and that phenomena is called chain isomerism (or) Nuclear isomerism.
Ex: 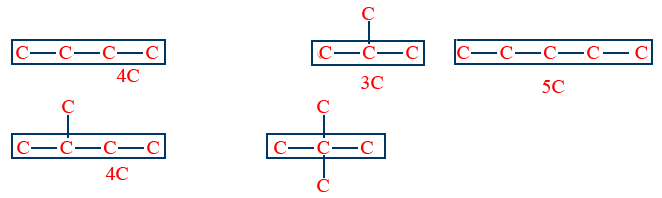
| Molecule | No. of chain isomers |
| Butane | 2 |
| Pentane | 3 |
| Hexane | 5 |
| Heptane | 9 |
| Octane | 18 |
| Nonane | 35 |
| Decane | 75 |
To exhibit chain isomerism, compound should have minimum '4' carbons.
Position Isomerism:
The isomers which differ in their position of functional groups (or) substituents (or) multiple bonds.
Ex: 
Functional Isomerism:
The isomers which differ in their functional groups are called functional isomers.
Ex: Alcohol and ethers (CnH2n+2 O)
CH3—CH2—OH and CH3—O—CH3
Cyanides and Isocyanides
CH3—CN and CH3—NC
Metamerism:
The isomers which differ in their alkyl groups which are linked to the functional groups
Ex: C—C—O—C—C Diethyl ether C—O—C—C—C methyl propyl ether
Ring Chain Isomerism:
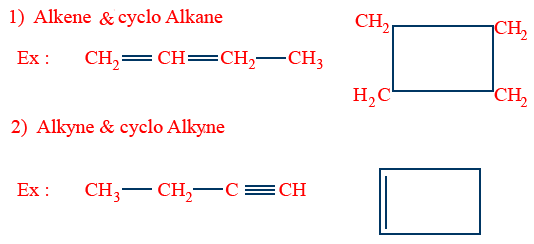
Tautomerism (Desmotropism)
Desmos = bond
tropism = turn
The Isomers which are in equilibrium state and they are inter convertible by transfer of hydrogen are called Tautomers.
Ex: 
Conditions for Tautomerism:
Compound should contain highly electronegative elements with multiple bonds (O,N)
Molecule contains α-hydrogens (acidic hydrogens)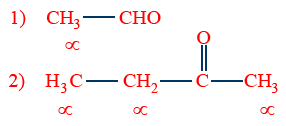
Stereo Isomerism:
The isomers which differ in their spatial arrangement of atoms (or) groups are called stereo isomers.
1.Geometrical Isomerism: (Cis-Trans Isomerism)
Isomerism arises mainly due to restricted rotation of {C=C}bond.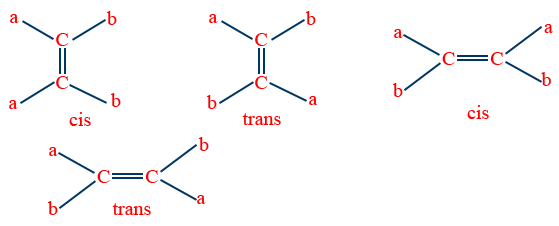
Note: The groups of the double bonded carbon should be different 
Properties of Cis-Trans Isomers:
1. Melting point Trans > Cis → Symmetrical
2. Boiling point Cis > Trans
3. Dipole moment (μ) Cis > Trans (μ=0)
4. Solubility Cis > Trans → Polar
5. Reactivity Cis > Trans
6. Stability Trans > Cis
E-Z nomenclature:
It is based on Cahn Ingold Prelog rules
a. If similar groups are at same side the isomer is called Z (Zussman) together
b. If similar groups are at opposite side that isomer is called E (Entgegan) opposite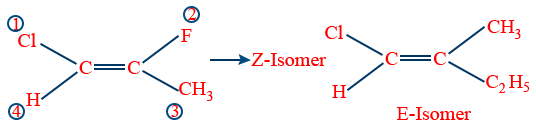
Optically Active Compound:
The compound which rotates the plane polarised light is called optical isomers.
(i) The isomer which rotates the plane polarised light towards right side is called dextro (d) or ⊕
(ii) If the isomer rotates plane polarised light towards left side is called laevo or (l)
Rules:
(iii) Molecule should be chiral (or) Asymmetric i.e, molecule has no symmetry and non superimposable on its mirror image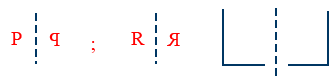
(iv) If molecule has any symmetry, which is superimposable on its mirror image is called Achiral.
Enantiomers:
The stereo isomers which are mirror images to each other are called enantiomers.
Ex: 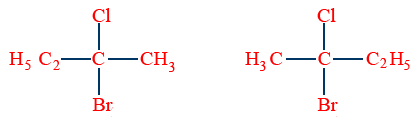
Diastereomer:
The stereo isomers which are non mirror images to each other are called diastereomers
Ex: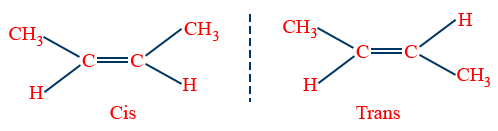
Meso Compound:
If molecules of half part is mirror image to the remaining half and it has a plane of symmetry to molecule is called meso compound.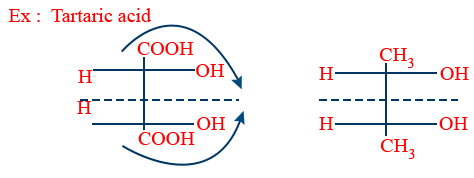
Meso compound due to internal compensation it is optically inactive.
Racemic Mixture:
Mixture containing 1:1 ratio of d and l (dextro and laevo) called racemic mixture (±1)
It is optically inactive due to external compensation formation of racemic mixture is called Racemisation.
Specific Rotation:
\tt \alpha =\frac{observer\ specific\ rotation}{length\ of\ tube(l\ in\ dm)\times conc\ of\ solution(gr/ml)}
\tt \left[\alpha\right]^T_\lambda=\frac{observer\ specific\ rotation}{l\times c}
No.of Geometrical Isomers:
1. Unsymmetry (ending different groups)
no. of G.I = 2n
2. Symmetrical (ending same groups)
Even no.of double bonds
G.I = 2n-1 + 2n/2-1
3. Odd no.of double bonds
\tt G.I=2^{n-1}+2^{\frac{n-1}{2}}
No. of optical Isomers (even no. of chiral carbons)
O.I = 2n-1
No.of meso forms = \tt 2^{\frac{n}{2}-1}
Total O.I = \tt 2^{n-1}+2^{\frac{n}{2}-1}
Odd no of chiral centers:
No. of optical Active form = \tt 2^{n-1}-2^{\frac{\left(n-1\right)}{2}}
No. of meso forms = \tt 2^{\frac{\left(n-1\right)}{2}}
Total O.I = 2(n-1)
Stability of chair form like structures:
Chair form > twist form > Boat form > Half chair
Part1: View the Topic in this Video from 49:01 to 57:18
Part2: View the Topic in this Video from 0:38 to 35:01
Disclaimer: Compete.etutor.co may from time to time provide links to third party Internet sites under their respective fair use policy and it may from time to time provide materials from such third parties on this website. These third party sites and any third party materials are provided for viewers convenience and for non-commercial educational purpose only. Compete does not operate or control in any respect any information, products or services available on these third party sites. Compete.etutor.co makes no representations whatsoever concerning the content of these sites and the fact that compete.etutor.co has provided a link to such sites is NOT an endorsement, authorization, sponsorship, or affiliation by compete.etutor.co with respect to such sites, its services, the products displayed, its owners, or its providers.
1. Number of optical active isomers = 2n (where, n = chiral carbon)
2. If two end are similar number of optical active isomers = 2n - 1 (if n = even) and meso form = 2(n - 2)/2.
3. If n = odd, number of optical active isomers = 2n-1 - 2(n - 1)/2.

